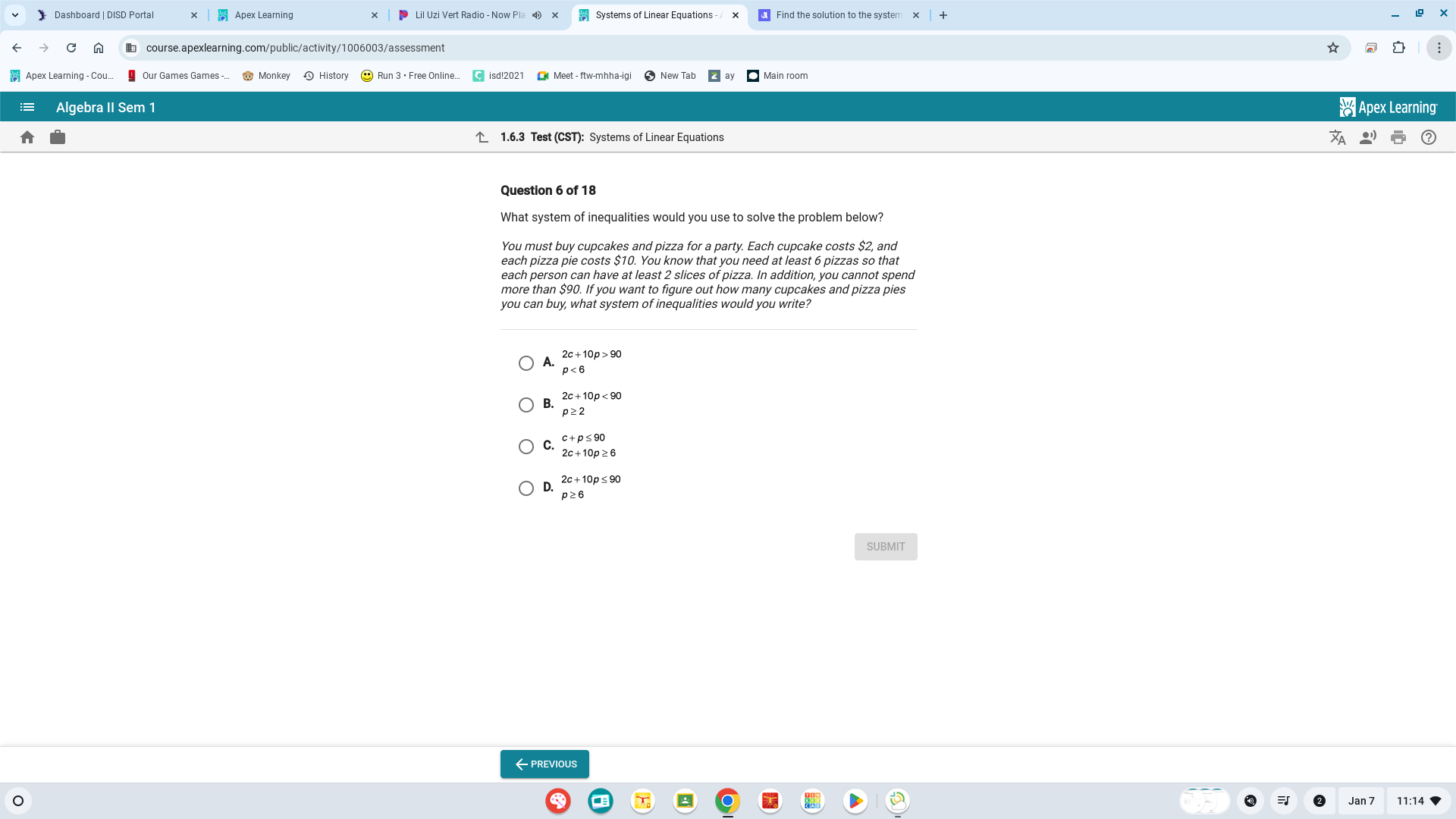
What system of inequalities would you use to solve the problem? You must buy cupcakes and pizza for a party. Each cupcake costs $2, and each pizza pie costs $10. You know that you... What system of inequalities would you use to solve the problem? You must buy cupcakes and pizza for a party. Each cupcake costs $2, and each pizza pie costs $10. You know that you need at least 6 pizzas so that each person can have at least 2 slices of pizza. In addition, you cannot spend more than $90. What system of inequalities would you write?
Understand the Problem
The question is asking which system of inequalities applies to a scenario involving the purchasing of cupcakes and pizza given their respective costs and quantities required. Specifically, it must capture the budget constraint and minimum requirements for pizza slices per person. We will analyze the choices to identify the correct inequalities for this problem.
Answer
The correct system of inequalities is \( 2c + 10p \leq 90 \) and \( p \geq 6 \).
Answer for screen readers
The correct set of inequalities is: $$ 2c + 10p \leq 90 \ p \geq 6 $$
Steps to Solve
-
Define Variables Let ( c ) represent the number of cupcakes, and ( p ) represent the number of pizza slices.
-
Establish Budget Constraint Each cupcake costs $2 and each pizza pie costs $10. The total cost must be less than or equal to $90. This leads to the inequality: $$ 2c + 10p \leq 90 $$
-
Set Minimum Slices Requirement Each person needs at least 2 slices of pizza. If we assume there are ( n ) people, then: $$ p \geq 2n $$ Assuming ( n ) is a variable that may be explicit in your problem, but in this case, we can define this requirement generally: $$ p \geq 6 $$ (for example, if there are 3 people needing at least 2 slices each, that totals 6 slices).
-
Combine Inequalities The inequalities based on the problem statement should represent the budget and needs:
- Budget: ( 2c + 10p \leq 90 )
- Minimum pizza requirement: ( p \geq 6 )
The correct set of inequalities is: $$ 2c + 10p \leq 90 \ p \geq 6 $$
More Information
This problem involves creating a system of inequalities based on costs and minimum requirements. Understanding these constraints is vital when budgeting and ensuring everyone is accommodated.
Tips
- Confusing inequalities: It's essential to correctly set up "less than or equal to" versus "greater than or equal to" based on the context.
- Not defining variables clearly: Properly defining what ( c ) and ( p ) represent is crucial for clarity.
AI-generated content may contain errors. Please verify critical information