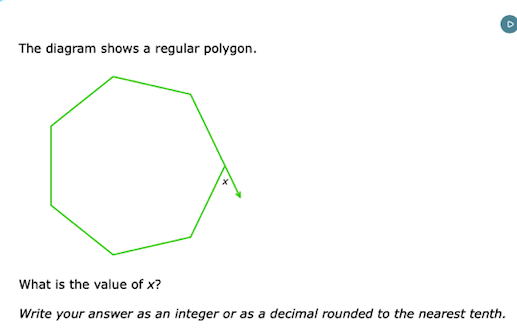
What is the value of x? Write your answer as an integer or as a decimal rounded to the nearest tenth.
Understand the Problem
The question is asking for the measure of the angle x in a regular polygon, specifically an octagon. To find x, we will need to calculate the interior angles of a regular octagon and then determine the specific value of x based on its configuration in the diagram.
Answer
$45^\circ$
Answer for screen readers
The value of $x$ is $45^\circ$.
Steps to Solve
- Calculate the sum of the interior angles of the octagon
For a polygon with $n$ sides, the formula for the sum of interior angles is given by: $$ \text{Sum of interior angles} = (n - 2) \times 180^\circ $$ For an octagon, where $n = 8$: $$ \text{Sum of interior angles} = (8 - 2) \times 180^\circ = 6 \times 180^\circ = 1080^\circ $$
- Determine the measure of one interior angle
Since the octagon is regular, each interior angle is: $$ \text{Interior angle} = \frac{\text{Sum of interior angles}}{n} = \frac{1080^\circ}{8} = 135^\circ $$
- Relationship of angles at vertex
From the diagram, the angle $x$ is formed such that it complements the interior angle at that corner. Therefore: $$ x + 135^\circ = 180^\circ $$
- Solve for angle x
To find the measure of angle $x$, we rearrange the equation: $$ x = 180^\circ - 135^\circ = 45^\circ $$
The value of $x$ is $45^\circ$.
More Information
In a regular octagon, each interior angle is $135^\circ$. Consequently, the exterior angle, which supplements the interior angle, simplifies to $45^\circ$. This relationship is a fundamental property of polygons.
Tips
- Misapplying the formula for the sum of the interior angles; it's essential to use $n-2$ for the correct calculation.
- Confusing interior and exterior angles; always remember that exterior angles are supplementary to interior angles.
AI-generated content may contain errors. Please verify critical information