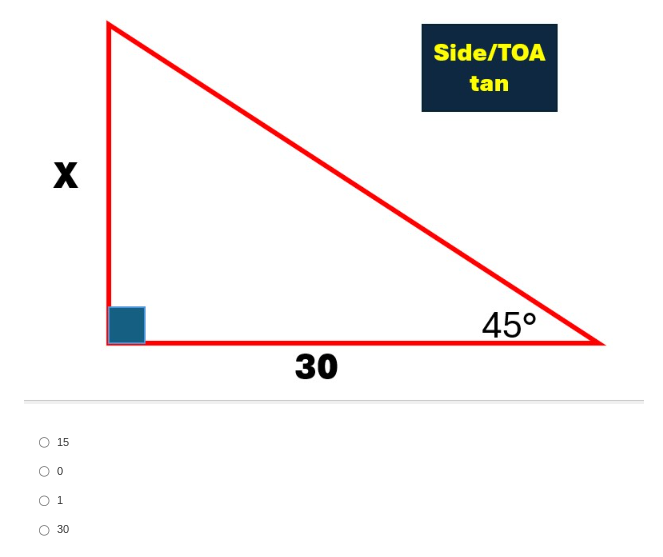
What is the value of X in the right triangle with a 45° angle and a side measuring 30?

Understand the Problem

The question is asking to find the value of 'X' in a right triangle using the tangent function. Given the angle of 45 degrees and one side measuring 30, we will use the tangent formula (tan = opposite/adjacent) to solve for X.

Answer

The value of $X$ is $30$.

Steps to Solve

Identify the tangent function Since we know the angle (45 degrees) and the length of the adjacent side (30), we can use the tangent function, which is defined as:

$$ \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} $$

Substitute known values Substituting the known values into the tangent function:

$$ \tan(45^\circ) = \frac{X}{30} $$

Evaluate the tangent of 45 degrees We know that:

$$ \tan(45^\circ) = 1 $$

Set up the equation Now, substitute the value of $\tan(45^\circ)$ into the equation:

$$ 1 = \frac{X}{30} $$

Solve for X To find (X), multiply both sides of the equation by 30:

$$ X = 1 \times 30 $$

This simplifies to:

$$ X = 30 $$

The value of (X) is (30).

More Information

In a right triangle with a 45-degree angle, both legs are equal in length when using the tangent function, and the tangent of 45 degrees is always 1. Therefore, if one side is 30, the other leg, (X), must also be 30.

Tips

Confusing the ratio for tangent; remember that for 45 degrees, both opposite and adjacent sides are equal.
Neglecting to convert the angle to degrees or radians can lead to incorrect results if tangent values are taken from the wrong context.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!