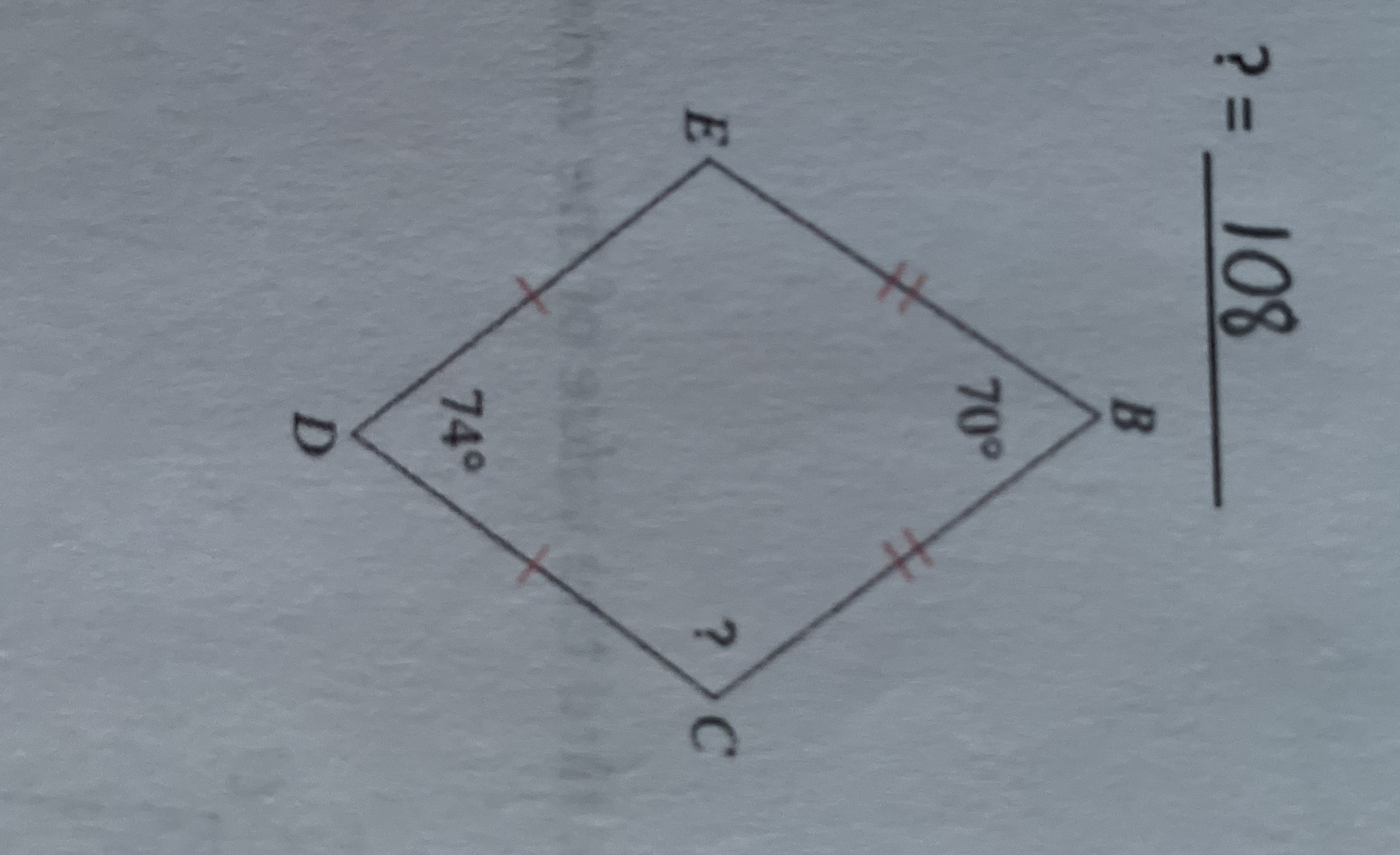
What is the value of the unknown angle in the parallelogram?
Understand the Problem
The question is asking to find the unknown angle in a parallelogram, using the properties of angles in a parallelogram, which state that opposite angles are equal, and adjacent angles are supplementary.
Answer
The unknown angle is $110^\circ$.
Answer for screen readers
The unknown angle is $110^\circ$.
Steps to Solve
- Identify given angles
The angles provided are:
- $\angle B = 70^\circ$
- $\angle D = 74^\circ$
- Use the property of supplementary angles
In a parallelogram, adjacent angles are supplementary, meaning they add up to $180^\circ$. Therefore, we can find $\angle A$:
$$ \angle A + \angle B = 180^\circ $$
Substituting in the known angle:
$$ \angle A + 70^\circ = 180^\circ $$
- Solve for angle A
Rearranging the equation to find $\angle A$:
$$ \angle A = 180^\circ - 70^\circ = 110^\circ $$
- Determine the unknown angle
Since opposite angles in a parallelogram are equal, $\angle C$ is the same as $\angle A$:
$$ \angle C = \angle A = 110^\circ $$
The unknown angle is $110^\circ$.
More Information
In a parallelogram, opposite angles are always equal, and adjacent angles are supplementary. This makes it easier to find unknown angles when some angles are given.
Tips
- Forgetting that opposite angles in a parallelogram are equal and that adjacent angles must sum to $180^\circ$.
- Not subtracting correctly when solving for the unknown angle.
AI-generated content may contain errors. Please verify critical information