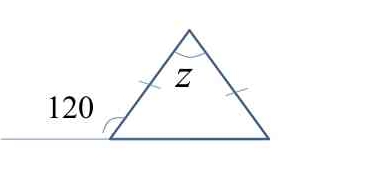
What is the value of angle Z in the triangle where one angle is 120 degrees?

Steps to Solve

1. Understand the triangle angle sum property

In any triangle, the sum of the interior angles is always $180^\circ$. This means we can use this property to find the unknown angle, $Z$.

2. Identify the known angle

We know that one of the angles in the triangle is $120^\circ$.

3. Set up the equation

Let's represent the unknown angle $Z$ and the third angle as $X$. According to the triangle angle sum property, we can write:

$$ Z + 120 + X = 180 $$

4. Simplify the equation

To find angle $Z$, we first need to express everything in terms of one unknown. Re-arranging the equation gives:

$$ Z + X = 180 - 120 $$

5. Calculate the value

Now we simplify the right side:

$$ Z + X = 60 $$

Since we have two unknowns ($Z$ and $X$), we can make a reasonable assumption to solve for $Z$ if more information isn't provided. However, as we only need to find $Z$ without specifically knowing $X$, we can write:

$$ Z = 60 - X $$

If we assume a common case where the other angle is also equal to $Z$ (for simplicity considering an isosceles triangle where both remaining angles are the same), we can let $Z = Z$:

$$ Z + Z = 60 $$

This leads to:

$$ 2Z = 60 $$

Thus:

$$ Z = 30 $$

6. Final conclusion

Therefore, under the assumed conditions, angle $Z$ is equal to $30^\circ$.