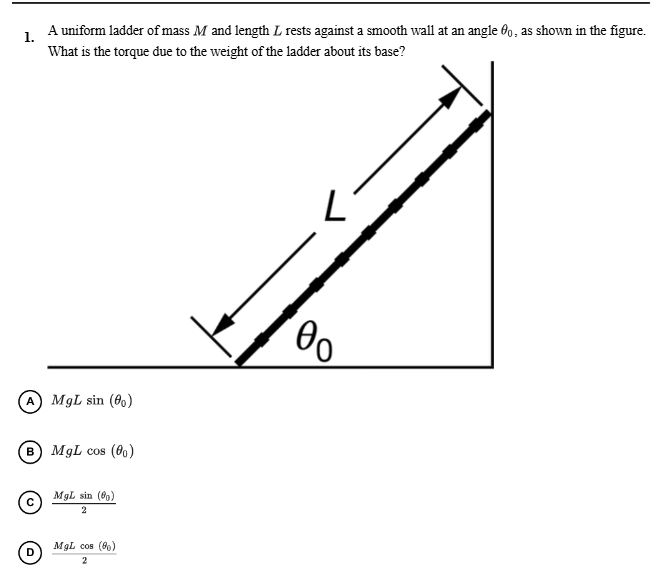
What is the torque due to the weight of the ladder about its base?
Understand the Problem
The question is asking for the torque due to the weight of a ladder resting against a wall, which can be calculated using the principles of physics. It involves understanding how to compute torque and the forces acting on the ladder at the angle θ₀.
Answer
$$ \frac{MgL}{2} \sin(\theta_0) $$
Answer for screen readers
$$ \tau = \frac{MgL}{2} \sin(\theta_0) $$
Steps to Solve
- Identify the Center of Mass of the Ladder
The center of mass of a uniform ladder is located at its midpoint, which is at a distance of $\frac{L}{2}$ from the base.
- Determine the Weight of the Ladder
The weight of the ladder can be calculated using the formula: $$ W = Mg $$ where $M$ is the mass of the ladder and $g$ is the acceleration due to gravity.
- Calculate the Distance from the Base to the Center of Mass
To find the distance from the base of the ladder to the point where the weight acts (the center of mass), we need to project this distance down to the horizontal: $$ d = \frac{L}{2} \cos(\theta_0) $$
- Calculate the Torque about the Base
The torque ($\tau$) due to the weight of the ladder about its base can be calculated using the formula: $$ \tau = r \times F $$ In this case, the force is the weight of the ladder ($W = Mg$), and $r$ is the horizontal distance from the base to the line of action of the weight, given by: $$ r = \frac{L}{2} \sin(\theta_0) $$ Thus, $$ \tau = \left( \frac{L}{2} \sin(\theta_0) \right) \cdot Mg $$
- Final Expression for Torque
Combining these, we get: $$ \tau = \frac{MgL}{2} \sin(\theta_0) $$
$$ \tau = \frac{MgL}{2} \sin(\theta_0) $$
More Information
The torque calculated reflects the rotational effect of the ladder's weight about its base. Torque is influenced by both the magnitude of the weight and the angle at which the ladder is resting.
Tips
- Confusing the angles when calculating the trigonometric functions; make sure to use $\sin(\theta_0)$ for vertical components related to torque.
- Forgetting to consider that the center of mass is at the halfway point of the ladder, leading to miscalculating the lever arm.
AI-generated content may contain errors. Please verify critical information