What is the surface area of the triangular prism, in square centimeters?
Understand the Problem
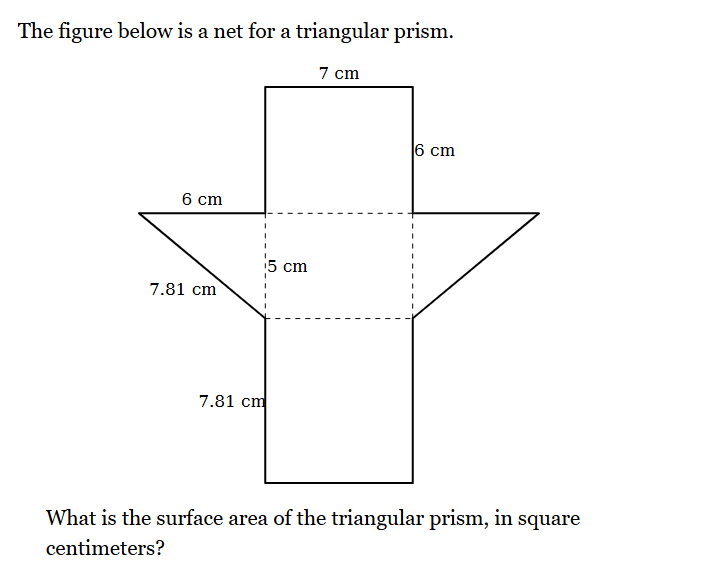
The question asks us to calculate the surface area of a triangular prism given its net. To do this, we need to identify all distinct faces of the net (two triangles and three rectangles) and calculate their areas individually by using the measurements provided. To calculate surface area we will sum up all areas together.
Answer
$181.34 \text{ cm}^2$
Answer for screen readers
$181.34 \text{ cm}^2$
Steps to Solve
- Calculate the area of one triangle
The area of a triangle is given by the formula $A = \frac{1}{2} \times base \times height$. In this case, the base of the triangle is 5 cm and the height is 6 cm. So, the area is:
$A = \frac{1}{2} \times 5 \times 6 = 15 \text{ cm}^2$
- Calculate the combined area of both triangles
Since there are two identical triangles, we multiply the area of one triangle by 2:
$2 \times 15 = 30 \text{ cm}^2$
- Calculate the area of the first rectangle
The area of the first rectangle is length $\times$ width $= 7 \times 6 = 42 \text{ cm}^2$
- Calculate the area of the second rectangle
The area of the second rectangle is length $\times$ width $= 7 \times 7.81 = 54.67 \text{ cm}^2$
- Calculate the area of the third rectangle
The area of the third rectangle is length $\times$ width $= 7 \times 7.81 = 54.67 \text{ cm}^2$
- Calculate the total area of the three rectangles
The total area of the rectangles is $42 + 54.67 + 54.67 = 151.34 \text{ cm}^2$
- Calculate the total surface area of the triangular prism
The surface area is the sum of the areas of the two triangles and the three rectangles:
$30 + 151.34 = 181.34 \text{ cm}^2$
$181.34 \text{ cm}^2$
More Information
The surface area of the triangular prism is $181.34 , \text{cm}^2$. This is found by calculating the areas of each face (2 triangles and 3 rectangles) and summing those areas together.
Tips
A common mistake is to forget to multiply the area of one triangle by 2 to account for both triangular faces. Another common mistake is calculating the area of the rectangles, confusing different dimensions. Finally, a mistake can arise from simply adding wrong or making a typo.
AI-generated content may contain errors. Please verify critical information