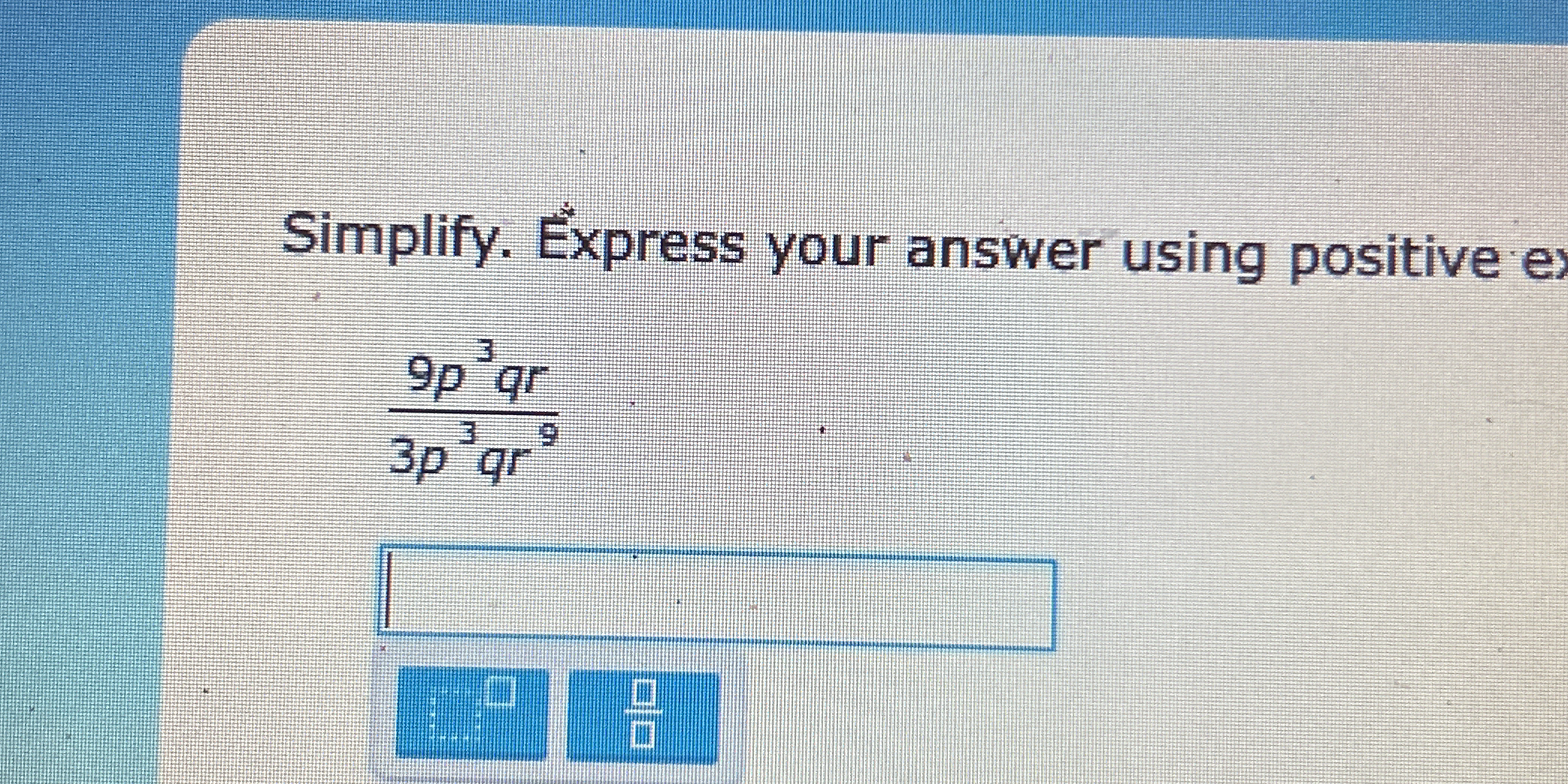
Simplify. Express your answer using positive exponents: 9p³qr / 3p³q⁹

Understand the Problem

The question asks us to simplify the expression 9p³qr / 3p³q⁹. To solve this, we will apply the rules of exponents and simplify the coefficients and variables step by step.

Answer

The simplified expression is $ \frac{3}{q^8} $.

Steps to Solve

Simplify the coefficients

Divide the coefficients (numerators and denominators):

$$ \frac{9}{3} = 3 $$

Simplify the variable ( p^3 )

Since both the numerator and denominator have the same variable ( p^3 ), they cancel each other out. Thus, we have:

$$ p^3 \div p^3 = 1 $$

Simplify the variable ( q )

Now, for the ( q ) terms, we subtract the exponent of the denominator from the exponent of the numerator using the rule ( q^{m-n} ):

$$ q^1 \div q^9 = q^{1 - 9} = q^{-8} $$

Combine results

Now, combining the simplified coefficients and variables, we have:

$$ \frac{3 \cdot 1 \cdot q^{-8}}{1} = 3q^{-8} $$

Express with positive exponents

To express the answer using positive exponents, we rewrite ( q^{-8} ):

$$ 3q^{-8} = \frac{3}{q^8} $$

The simplified expression is ( \frac{3}{q^8} ).

More Information

When simplifying expressions with variables and exponents, remember to apply the rules of exponents carefully and to express all variables with positive exponents if necessary. This is a common requirement in algebra to keep expressions tidy and standardized.

Tips

Forgetting to simplify coefficients: Always check if the coefficients can be simplified before simplifying variables.
Misapplying exponent rules: Remember that when dividing with the same base, you subtract the exponents.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!