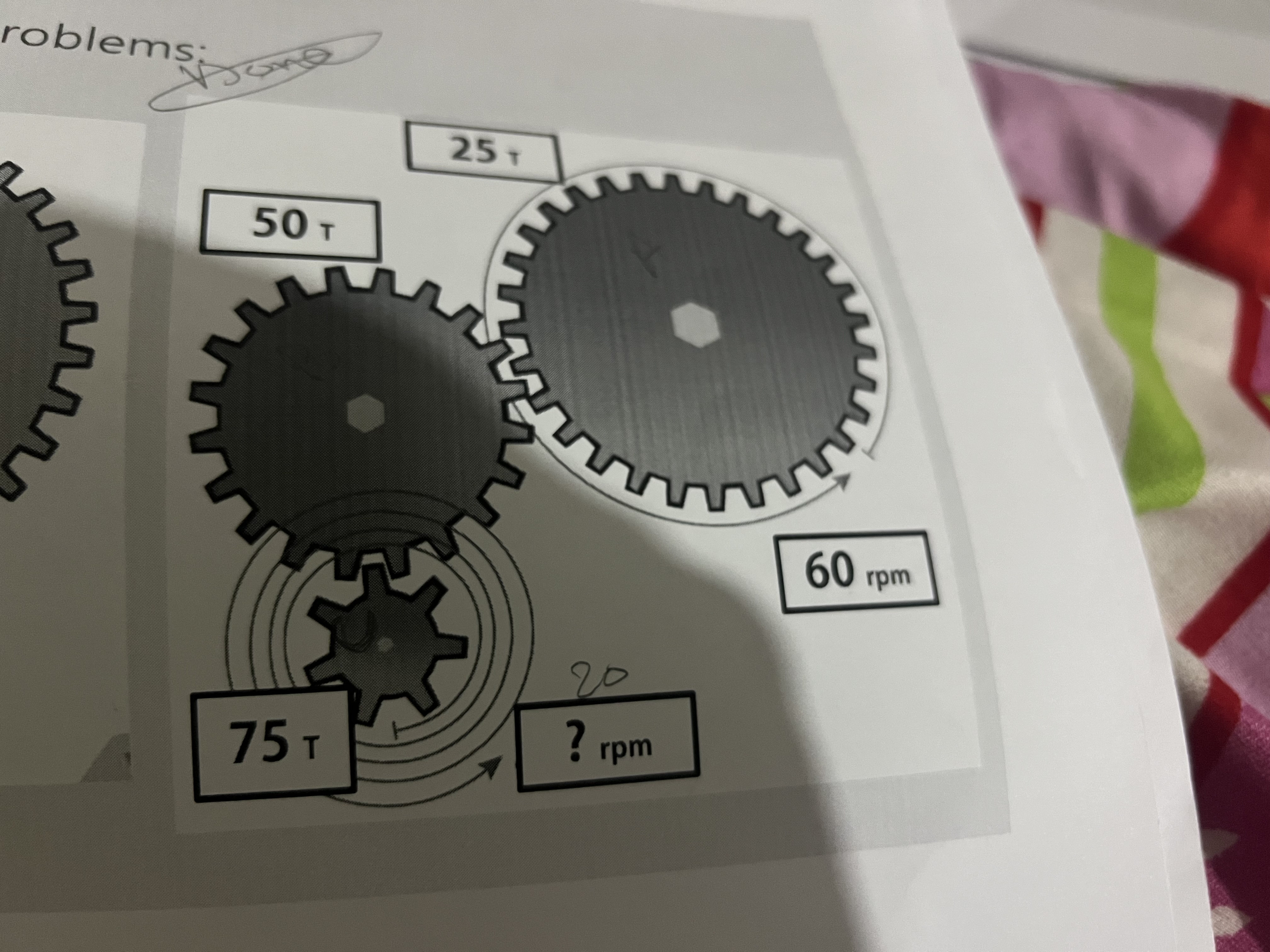
What is the RPM of the gear with 75 teeth given that the gear with 50 teeth is turning at 60 RPM?
Understand the Problem
The question relates to calculating the rotational speed of a gear system involving multiple gears with different tooth counts and known RPM. It requires applying principles of gear ratios to find the unknown RPM.
Answer
The RPM of the 75-tooth gear is $40$ RPM.
Answer for screen readers
The RPM of the 75-tooth gear is 40 RPM.
Steps to Solve
- Identify the gears and their relationships
The gear system has a 75-tooth gear (let's call it Gear A) and a 50-tooth gear (let's call it Gear B). Gear B is turning at 60 RPM.
- Use the gear ratio to relate RPMs
The gear ratio can be expressed as: $$ \text{Gear Ratio} = \frac{\text{Teeth on Gear B}}{\text{Teeth on Gear A}} = \frac{50}{75} $$
- Calculate the speed of Gear A
The RPM of Gear A (the unknown) can be found using the formula: $$ \text{RPM of Gear A} = \text{RPM of Gear B} \times \frac{\text{Teeth on Gear B}}{\text{Teeth on Gear A}} $$
Substituting the values: $$ \text{RPM of Gear A} = 60 \times \frac{50}{75} $$
- Perform the calculation
Now, calculate the RPM of Gear A: $$ \text{RPM of Gear A} = 60 \times \frac{50}{75} = 60 \times \frac{2}{3} = 40 \text{ RPM} $$
The RPM of the 75-tooth gear is 40 RPM.
More Information
In a gear system, the RPM of a gear decreases when it has more teeth in comparison to its driving gear. In this case, the 75-tooth gear rotates slower than the 50-tooth gear due to more teeth meshing.
Tips
- Confusing the direction of rotation: It's important to remember that gears rotate in opposite directions.
- Not simplifying the gear ratio correctly before calculations: Always simplify fractions before performing multiplications.
AI-generated content may contain errors. Please verify critical information