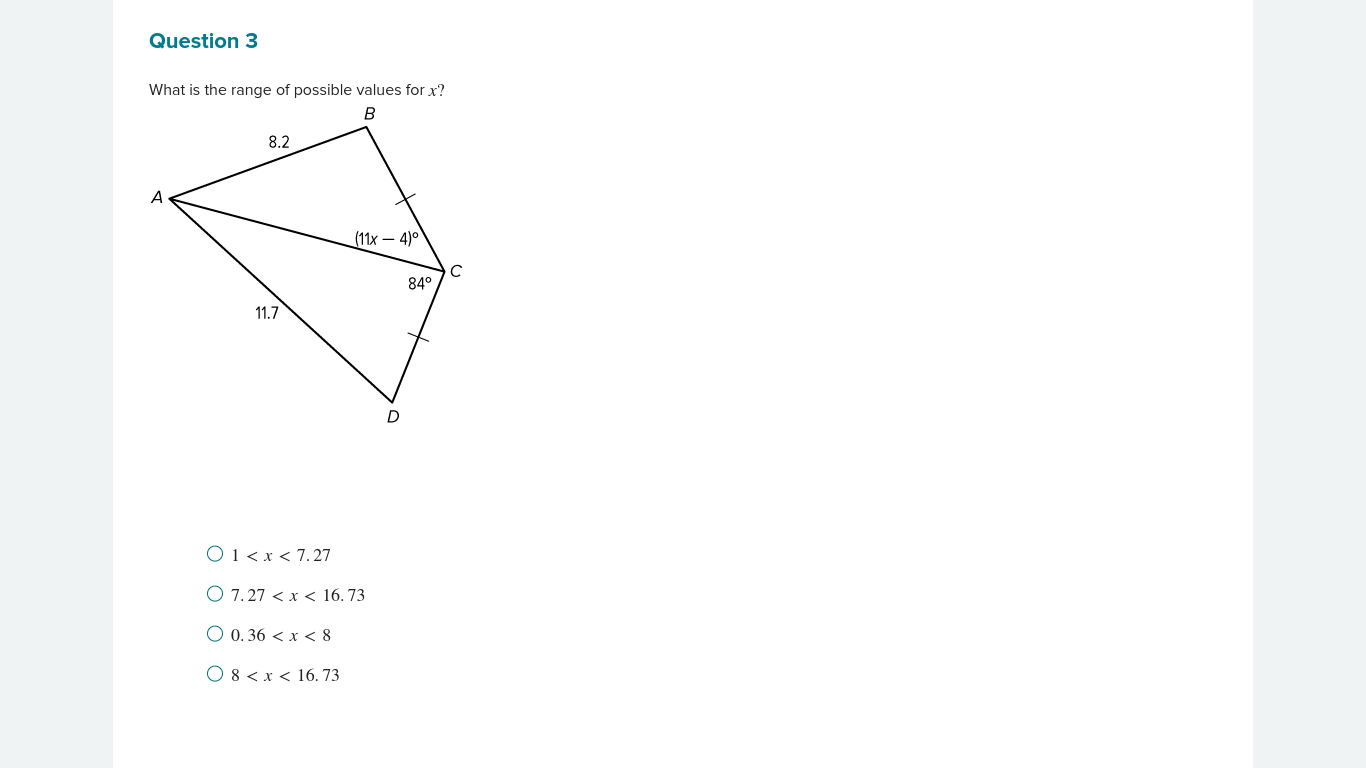
What is the range of possible values for x?

Steps to Solve

1. Identify the angles of the quadrilateral

In a quadrilateral, the sum of all interior angles is $360^\circ$. The angles we have are $(11x - 4)^\circ$, $84^\circ$, and the angle at vertex D, which we can find out by letting it be $y^\circ$. Thus, we can set up the following equation:

$$ (11x - 4) + 84 + y = 360 $$

2. Express y in terms of x

Rearranging the equation, we find:

$$ y = 360 - (11x - 4 + 84) $$

Simplifying this gives:

$$ y = 360 - (11x + 80) = 280 - 11x $$

3. Set up the conditions for y

Since angles in a quadrilateral must be positive, we have:

$$ 280 - 11x > 0 $$

Solving for $x$ gives:

$$ 280 > 11x \implies x < \frac{280}{11} \approx 25.45 $$

4. Set up the condition for the first angle

The angle $(11x - 4)^\circ$ must also be positive:

$$ 11x - 4 > 0 $$

Solving this gives:

$$ 11x > 4 \implies x > \frac{4}{11} \approx 0.36 $$

5. Combine the conditions

Now, we combine the two conditions:

• From the angle $(11x - 4)^\circ$: $x > 0.36$
• From the angle at vertex D: $x < 25.45$

Hence, the combined inequality is:

$$ 0.36 < x < 25.45 $$

Now, since the only relevant options provided in the choices are between numbers less than 25.45, we look for the correct range that fits our derived inequality.