What is the missing number? 3/10 + 7/100 = ___/100
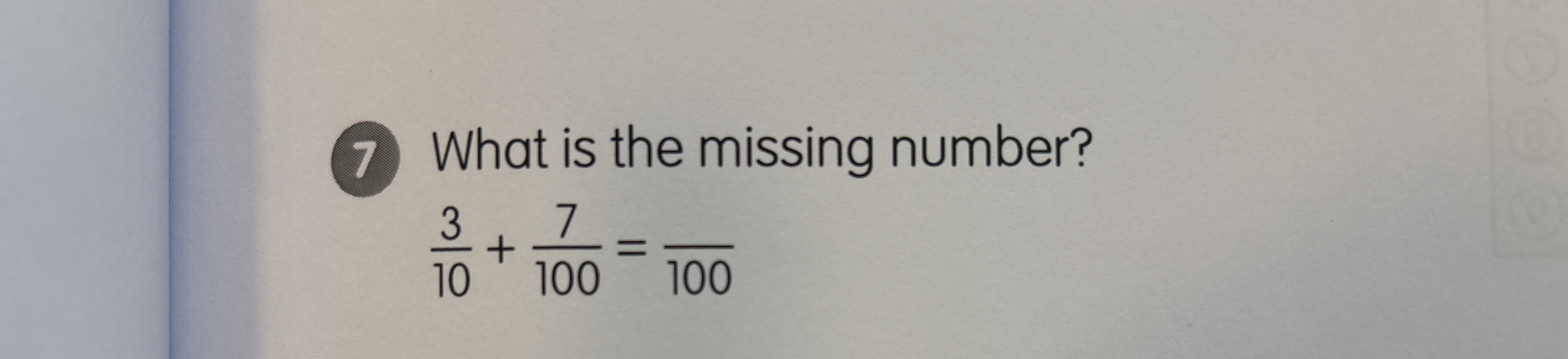
Understand the Problem
The question is asking to find the missing number that completes the equation involving the fractions 3/10 and 7/100. The goal is to determine what number over 100, when added to 3/10 and 7/100, equals a whole number or fraction.
Answer
The missing number is 37.
Answer for screen readers
The missing number is 37.
Steps to Solve
-
Convert 3/10 to a fraction with a denominator of 100 To add the fractions, we need a common denominator. The denominator for the first fraction is 10, so we can convert it to an equivalent fraction with a denominator of 100 by multiplying both the numerator and denominator by 10:
$$ \frac{3}{10} = \frac{3 \times 10}{10 \times 10} = \frac{30}{100} $$
-
Add the converted fraction to 7/100 Now, we can add the two fractions together:
$$ \frac{30}{100} + \frac{7}{100} = \frac{30 + 7}{100} = \frac{37}{100} $$
-
Identify the missing number The equation states that the sum equals some number over 100:
$$ \frac{3}{10} + \frac{7}{100} = \frac{37}{100} $$ Thus, the missing number is 37.
The missing number is 37.
More Information
When adding fractions, it's crucial to have a common denominator. In this case, converting 3/10 to an equivalent fraction with a denominator of 100 allows for straightforward addition with 7/100.
Tips
- Forgetting to convert fractions to a common denominator before adding.
- Miscalculating during the addition of fractions, leading to incorrect answers.
AI-generated content may contain errors. Please verify critical information