What is the magnitude of the acceleration of the blocks?
Understand the Problem
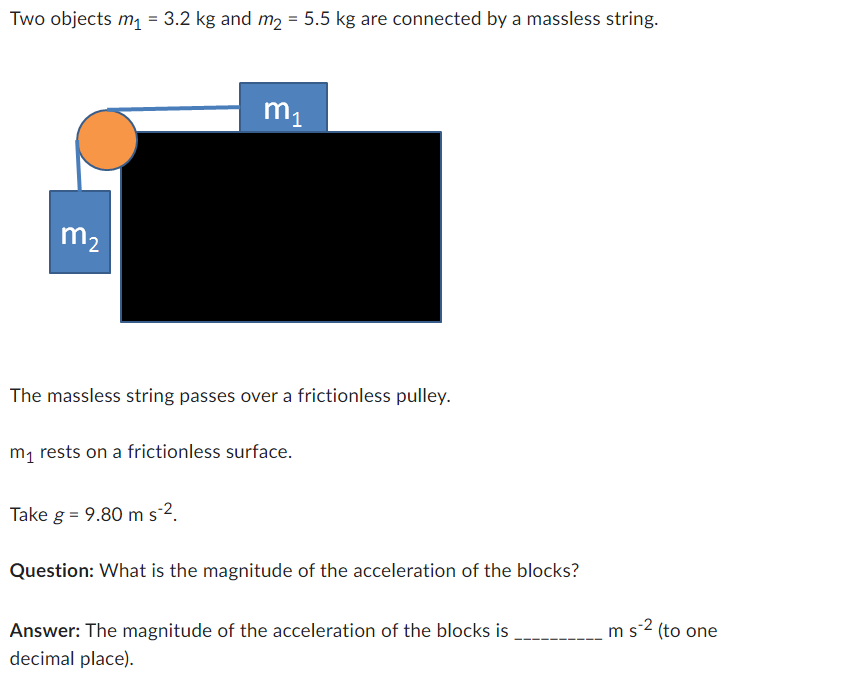
The question is asking for the magnitude of the acceleration of two connected blocks, where one is on a frictionless surface and the other is hanging. To solve this, we need to use Newton's second law and consider the forces acting on both masses.
Answer
The magnitude of the acceleration of the blocks is $6.2 \, \text{m/s}^2$.
Answer for screen readers
The magnitude of the acceleration of the blocks is approximately $6.2 , \text{m/s}^2$.
Steps to Solve
- Identify the Forces Acting on Each Block
For block $m_1$ (mass $3.2 , \text{kg}$), which is on a frictionless surface, the only forces acting on it are the tension $T$ in the string pulling it to the right.
For block $m_2$ (mass $5.5 , \text{kg}$), which is hanging, the forces acting on it are the gravitational force $m_2 g$ (downward) and the tension $T$ (upward).
- Write Down the Equations Based on Newton's Second Law
For block $m_1$: $$ T = m_1 a $$ This equation states that the tension in the string provides the acceleration $a$ to block $m_1$.
For block $m_2$: $$ m_2 g - T = m_2 a $$ This equation expresses that the weight of block $m_2$ minus the tension $T$ in the string is equal to the mass times its acceleration.
- Substitute Known Values and Rearrange the Equations
From the first equation, substitute $T$ into the second equation: $$ m_2 g - m_1 a = m_2 a $$
Rearranging this gives: $$ m_2 g = m_2 a + m_1 a $$
- Factor and Solve for Acceleration $a$
Factor out $a$ on the right side: $$ m_2 g = (m_1 + m_2) a $$
Then, solve for $a$: $$ a = \frac{m_2 g}{m_1 + m_2} $$
- Substitute the Values into the Equation
Substituting the known values: $$ a = \frac{5.5 , \text{kg} \times 9.80 , \text{m/s}^2}{3.2 , \text{kg} + 5.5 , \text{kg}} $$
- Calculate the Result
Calculate the values: $$ a = \frac{53.9}{8.7} \approx 6.2 , \text{m/s}^2 $$
The magnitude of the acceleration of the blocks is approximately $6.2 , \text{m/s}^2$.
More Information
The acceleration calculated indicates how fast the blocks are speeding up due to the force of gravity acting on the hanging block $m_2$. This scenario is a classic example of using Newton's second law in a connected mass system involving pulleys.
Tips
- Forgetting to account for the direction of the acceleration.
- Not properly distinguishing between the forces on each block.
- Incorrectly simplifying the equations, which can lead to an incorrect value for acceleration.
AI-generated content may contain errors. Please verify critical information