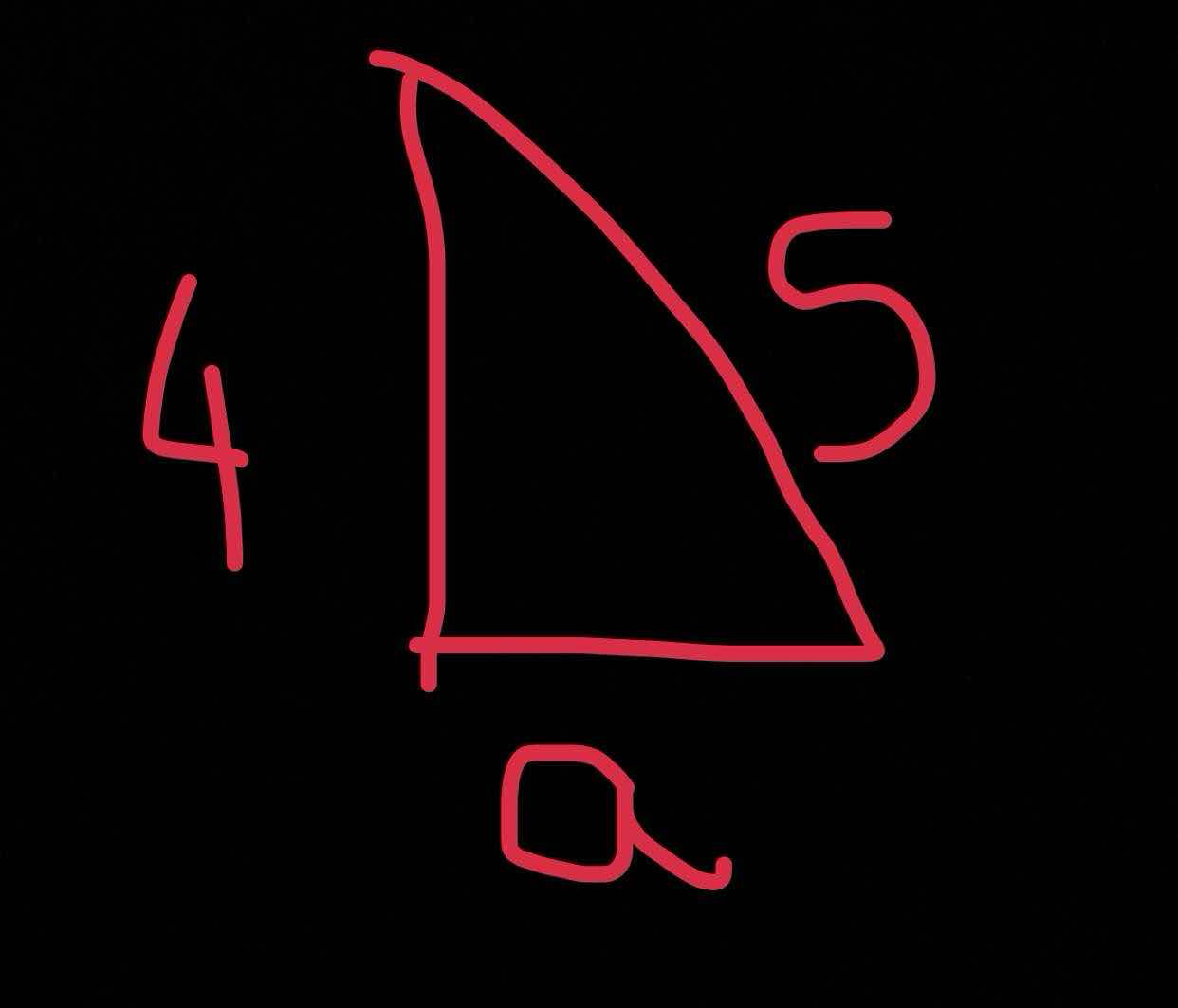
What is the length of side 'a' in a right triangle with one side measuring 4 and the hypotenuse measuring 5?
Understand the Problem
The question is asking for the missing length 'a' in a right triangle with one side measuring 4 units and the hypotenuse measuring 5 units. We can solve this using the Pythagorean theorem.
Answer
The length of side 'a' is $3$.
Answer for screen readers
The length of side 'a' is $3$.
Steps to Solve
-
Identify the Pythagorean Theorem The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse ($c$) is equal to the sum of the squares of the lengths of the other two sides ($a$ and $b$). The formula is given by: $$ c^2 = a^2 + b^2 $$
-
Substitute known values into the equation In this problem, we know one side ($b = 4$) and the hypotenuse ($c = 5$). We need to find the other side ($a$). Substituting these values into the theorem gives: $$ 5^2 = a^2 + 4^2 $$
-
Calculate $c^2$ and $b^2$ Now, let's calculate the squares: $$ 5^2 = 25 $$ $$ 4^2 = 16 $$
-
Set up the equation Substituting the calculated values back into the equation: $$ 25 = a^2 + 16 $$
-
Isolate $a^2$ Now, we need to isolate $a^2$: $$ a^2 = 25 - 16 $$
-
Perform the subtraction Calculating the right-hand side: $$ a^2 = 9 $$
-
Find $a$ by taking the square root Finally, take the square root to find the length of side $a$: $$ a = \sqrt{9} $$
-
Calculate the final value Thus, we get: $$ a = 3 $$
The length of side 'a' is $3$.
More Information
In this right triangle, the relationship between the sides defines a fundamental concept in geometry. This scenario is a classic example of the Pythagorean theorem, often used in various real-world applications, such as construction and navigation.
Tips
- Forgetting to square the sides correctly: Ensure the squares are computed accurately.
- Ignoring the positive root: When taking the square root, always consider the positive value, as a length cannot be negative.
AI-generated content may contain errors. Please verify critical information