What is the determinant of the matrix |3 3| |1 2|?

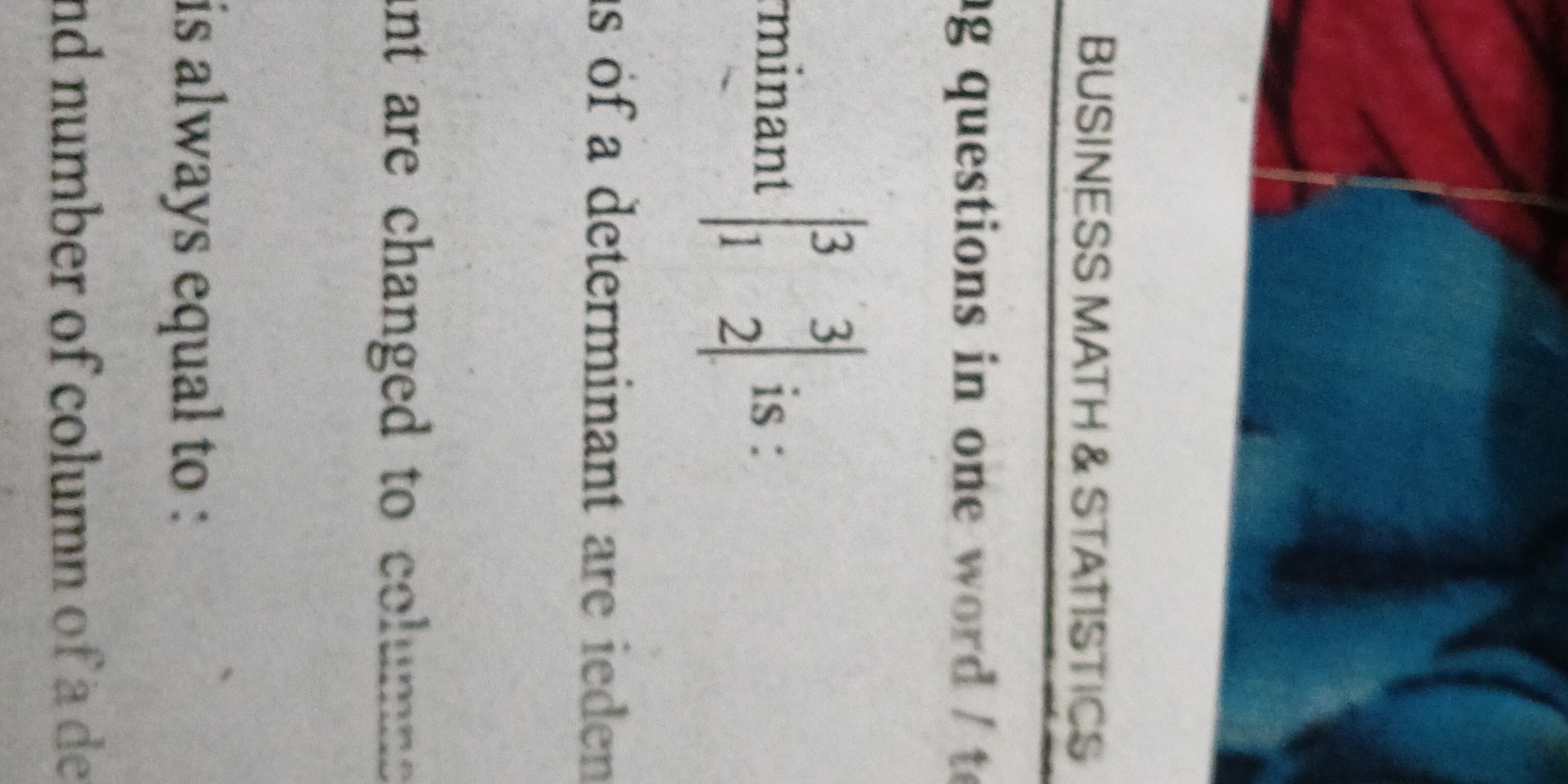
Understand the Problem

The question asks for the value of the determinant of a given 2x2 matrix. The matrix provided is |3 3| |1 2|, and we need to calculate its determinant.

Answer

The determinant of the matrix is $ 3 $.

Steps to Solve

Identify the matrix

The given matrix is

$$ \begin{pmatrix} 3 & 3 \ 1 & 2 \end{pmatrix} $$

Use the formula for the determinant of a 2x2 matrix

The formula for the determinant of a 2x2 matrix

$$ \begin{pmatrix} a & b \ c & d \end{pmatrix} $$

is given by

$$ \text{det} = ad - bc $$

In this case, we have:

$a = 3$,
$b = 3$,
$c = 1$,
$d = 2$

Substitute the values into the determinant formula

Now, substitute the values into the determinant formula:

$$ \text{det} = (3)(2) - (3)(1) $$

Calculate the expression

First, calculate the products:

$(3)(2) = 6$
$(3)(1) = 3$

Now, substitute back into the expression:

$$ \text{det} = 6 - 3 $$

Final calculation

Perform the subtraction:

$$ \text{det} = 3 $$

The value of the determinant is ( 3 ).

More Information

The determinant of a 2x2 matrix provides information about the matrix, such as whether it is invertible. If the determinant is non-zero (like in this case), the matrix is invertible. If it were zero, it would indicate that the matrix is singular.

Tips

A common mistake is mixing up the multiplication or forgetting to subtract properly in the determinant calculation. Always double-check each multiplication and the final subtraction.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!