What is the derivative of u = 6054t with respect to t?
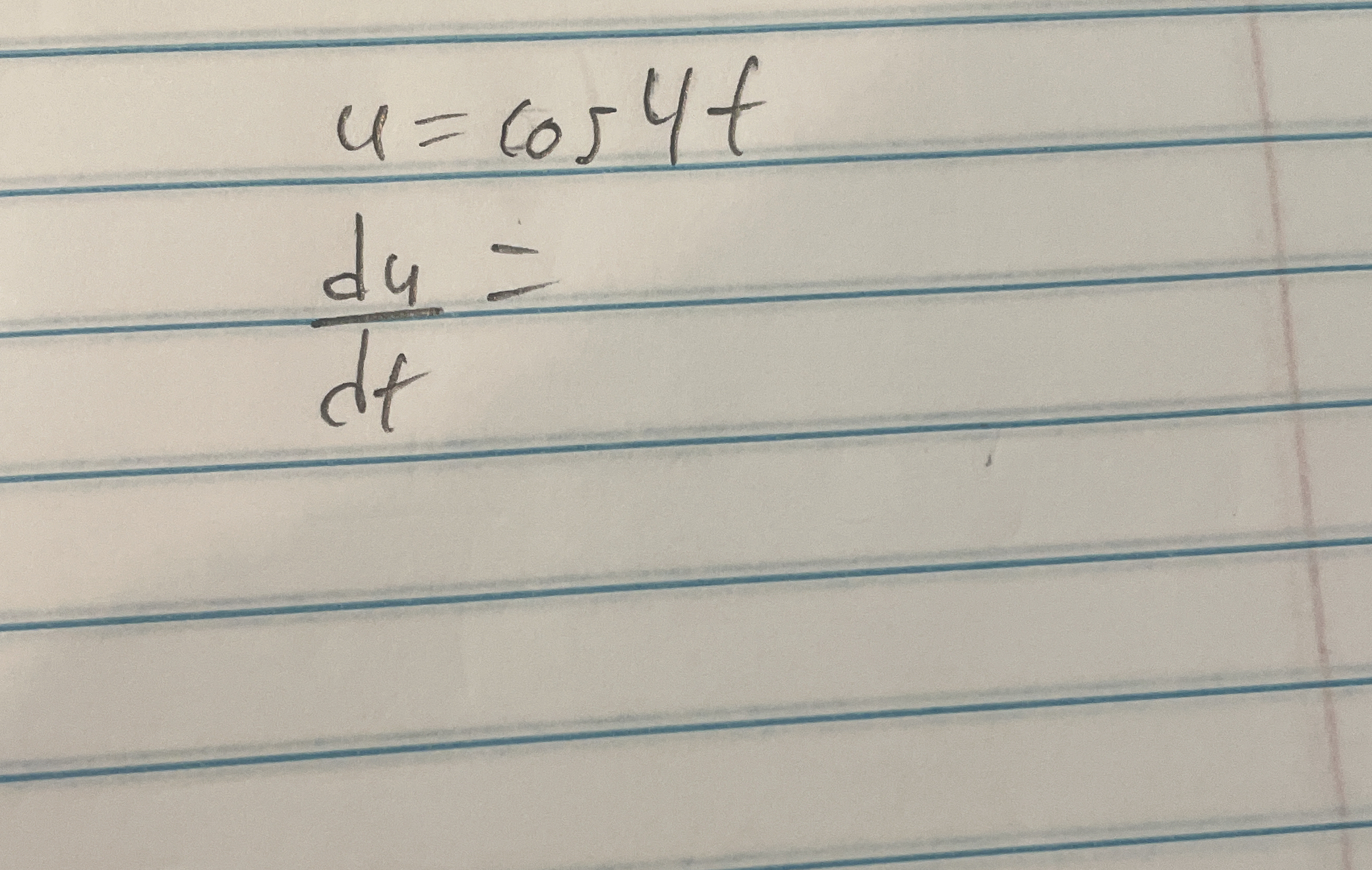
Understand the Problem
The question appears to be seeking guidance on how to find the derivative of the function u with respect to time t, as indicated by the notation dy/dt.
Answer
$$ \frac{du}{dt} = 6054 $$
Answer for screen readers
$$ \frac{du}{dt} = 6054 $$
Steps to Solve
-
Identify the function to differentiate We have the function ( u = 6054t ).
-
Apply the derivative rules The derivative of a constant multiplied by a variable ( t ) is simply the constant itself. Hence,
$$ \frac{du}{dt} = 6054 $$
- Conclusion The derivative ( \frac{du}{dt} ) is the rate of change of ( u ) with respect to ( t ).
$$ \frac{du}{dt} = 6054 $$
More Information
The derivative ( \frac{du}{dt} ) indicates that for every unit increase in ( t ), the value of ( u ) increases by 6054.
Tips
- Confusing the variable ( u ) with ( y ) and mislabeling the derivative.
- Forgetting that the derivative of ( kt ) (where ( k ) is a constant) is simply ( k ).
AI-generated content may contain errors. Please verify critical information
Thank you for voting!
