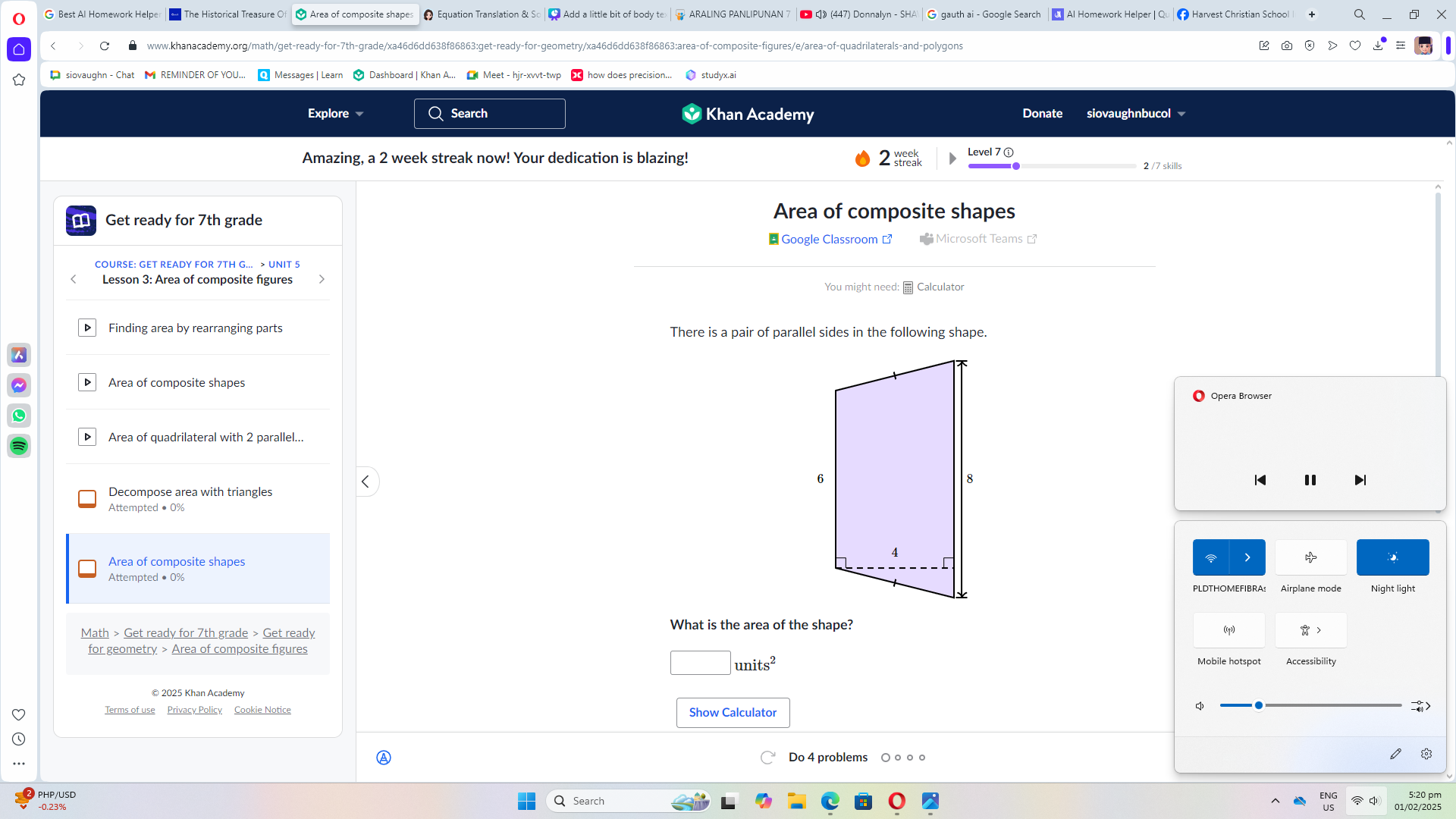
What is the area of the shape?
Understand the Problem
The question is asking for the area of a composite shape, which includes dimensions given for the sides. To solve it, we would need to use the provided dimensions and apply the appropriate formula for calculating the area.
Answer
The area of the shape is $24 \text{ units}^2$.
Answer for screen readers
The area of the shape is $24 \text{ units}^2$.
Steps to Solve
- Identify the shape and dimensions
The shape appears to be a composite figure made of rectangles. We see two dimensions, 6 units and 8 units, visible on the vertical and horizontal sides, respectively. Also, the rectangle has a smaller side measuring 4 units.
- Calculate the area of the large rectangle
The area of a rectangle can be calculated using the formula:
$$ \text{Area} = \text{length} \times \text{width} $$
For the larger rectangle formed by the height of 8 units and the base of 4 units:
$$ \text{Area}_{\text{large}} = 8 \times 6 = 48 \text{ units}^2 $$
- Calculate the area of the small rectangle
Now, we need to find the area of the smaller rectangle, which has dimensions for width as 4 units and height as 6 units. Therefore:
$$ \text{Area}_{\text{small}} = 4 \times 6 = 24 \text{ units}^2 $$
- Calculate the total area of the composite shape
To find the total area of the composite shape, we add the areas of the two rectangles:
$$ \text{Total Area} = \text{Area}{\text{large}} - \text{Area}{\text{small}} = 48 - 24 = 24 \text{ units}^2 $$
The area of the shape is $24 \text{ units}^2$.
More Information
The area represents the total space covered by the composite figure. This exercise helps to build skills in decomposing shapes into simpler parts and calculating their areas individually.
Tips
- Not correctly identifying the dimensions of each part of the composite figure.
- Forgetting to subtract the area of the smaller shape from the area of the larger shape when needed.
AI-generated content may contain errors. Please verify critical information