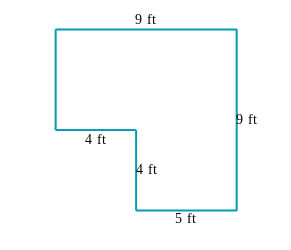
What is the area of the given shape?
Understand the Problem
The question is asking for the area of a composite shape given its dimensions. To find the area, we can divide the shape into simpler rectangles, calculate the area of each rectangle, and then sum them.
Answer
The total area of the composite shape is \( 101 \, \text{ft}^2 \).
Answer for screen readers
The total area of the composite shape is ( 101 , \text{ft}^2 ).
Steps to Solve
- Divide the shape into rectangles
To find the area of the composite shape, we can divide it into two rectangles. The first rectangle on top and the second rectangle on the bottom.
- Calculate the dimensions of the rectangles
- For the top rectangle:
- Width = 9 ft
- Height = 9 ft
- For the bottom rectangle:
- Width = 5 ft (given)
- Height = 4 ft (given)
- Calculate the area of each rectangle
- Area of the top rectangle:
$$ \text{Area}{\text{top}} = \text{Width}{\text{top}} \times \text{Height}_{\text{top}} = 9 , \text{ft} \times 9 , \text{ft} = 81 , \text{ft}^2 $$
- Area of the bottom rectangle:
$$ \text{Area}{\text{bottom}} = \text{Width}{\text{bottom}} \times \text{Height}_{\text{bottom}} = 5 , \text{ft} \times 4 , \text{ft} = 20 , \text{ft}^2 $$
- Sum the areas
Now, add the areas of both rectangles to get the total area of the composite shape:
$$ \text{Total Area} = \text{Area}{\text{top}} + \text{Area}{\text{bottom}} = 81 , \text{ft}^2 + 20 , \text{ft}^2 = 101 , \text{ft}^2 $$
The total area of the composite shape is ( 101 , \text{ft}^2 ).
More Information
The approach of breaking down complex shapes into simpler rectangles is a common technique in geometry. It simplifies calculations and makes it easier to find areas of irregular shapes.
Tips
- Not correctly identifying the dimensions of each rectangle.
- Forgetting to sum the areas of the rectangles.
- Mixing up the width and height when multiplying to find area.
AI-generated content may contain errors. Please verify critical information