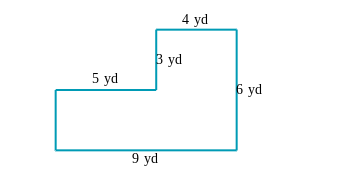
What is the area of the given L-shaped figure?
Understand the Problem
The question appears to be about calculating the area of the given L-shaped figure with various dimensions labeled in yards. We will use the provided dimensions to find the total area by breaking the shape into smaller rectangles.
Answer
The total area of the L-shaped figure is \(69 \, \text{yd}^2\).
Answer for screen readers
The total area of the L-shaped figure is (69 , \text{yd}^2).
Steps to Solve
- Identify the dimensions of the rectangles
The L-shaped figure can be divided into two rectangles. The first rectangle has dimensions 9 yd by 5 yd, and the second rectangle has dimensions 4 yd by 6 yd.
- Calculate the area of the first rectangle
To find the area of the first rectangle, use the formula for the area of a rectangle:
[ \text{Area} = \text{length} \times \text{width} ]
For the first rectangle:
[ \text{Area}_1 = 9 , \text{yd} \times 5 , \text{yd} = 45 , \text{yd}^2 ]
- Calculate the area of the second rectangle
Now calculate the area of the second rectangle using the same formula:
[ \text{Area}_2 = 4 , \text{yd} \times 6 , \text{yd} = 24 , \text{yd}^2 ]
- Add the areas of both rectangles
The total area of the L-shaped figure is the sum of the areas of both rectangles:
[ \text{Total Area} = \text{Area}_1 + \text{Area}_2 = 45 , \text{yd}^2 + 24 , \text{yd}^2 = 69 , \text{yd}^2 ]
The total area of the L-shaped figure is (69 , \text{yd}^2).
More Information
The area calculation involves breaking down complex shapes into simpler rectangles. The concept of area is fundamental in geometry and applied in various real-world contexts, such as landscaping and architecture.
Tips
- Forgetting to break the shape into rectangles before calculating areas.
- Mixing up the dimensions when calculating areas of the rectangles.
- Adding areas incorrectly.
AI-generated content may contain errors. Please verify critical information