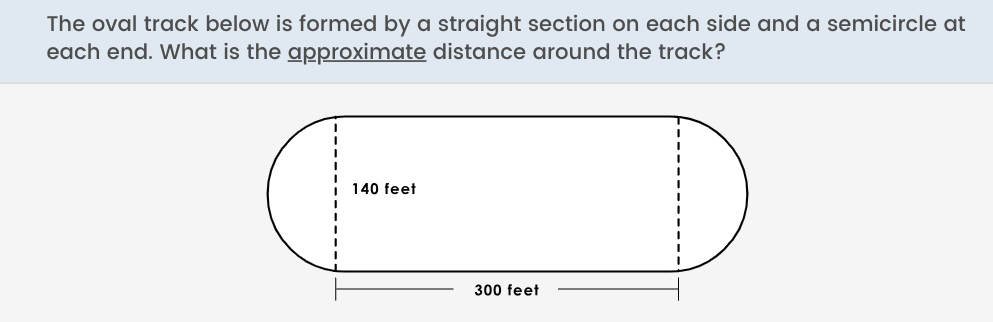
What is the approximate distance around the track?
Understand the Problem
The question is asking to calculate the approximate distance around an oval track that consists of straight sections and semicircles. To solve this, we will first determine the length of the two straight sections and then calculate the circumference of the two semicircles, which together will form a full circle.
Answer
The approximate distance around the track is $1039.6$ feet.
Answer for screen readers
The approximate distance around the track is $1039.6$ feet.
Steps to Solve
-
Identify the lengths of the straight sections The track has two straight sections, each measuring 300 feet. Thus, the total length from the straight sections is: $$ \text{Total straight length} = 2 \times 300 = 600 \text{ feet} $$
-
Determine the radius of the semicircles The width of the track dictates the diameter of each semicircle. Since the straight sections are each 140 feet: $$ \text{Diameter of semicircles} = 140 \text{ feet} \ \text{Radius} = \frac{140}{2} = 70 \text{ feet} $$
-
Calculate the circumference of a full circle To find the total length of both semicircles, first calculate the circumference of a full circle using the formula (C = 2\pi r): $$ C = 2 \pi (70) = 140\pi \text{ feet} $$
-
Calculate the total distance around the track Add the lengths of the straight sections and the full circle (circumference of the two semicircles): $$ \text{Total distance} = \text{Total straight length} + \text{Circumference} \ \text{Total distance} = 600 + 140\pi $$
-
Approximate the total distance Using an approximation for (\pi \approx 3.14): $$ \text{Total distance} \approx 600 + 140 \times 3.14 \approx 600 + 439.6 = 1039.6 \text{ feet} $$
The approximate distance around the track is $1039.6$ feet.
More Information
This calculation combines the lengths of straight sections with the circumferences of semicircles to provide a realistic measure of the oval track's total distance. Understanding how to break down complex shapes into simpler components is essential in geometry.
Tips
- Forgetting to double the straight sections; it’s easy to overlook both sides when measuring.
- Incorrectly calculating the radius from the diameter; always divide by 2.
- Failing to use an approximate value for (\pi); ensure to estimate correctly when needing numerical answers.
AI-generated content may contain errors. Please verify critical information