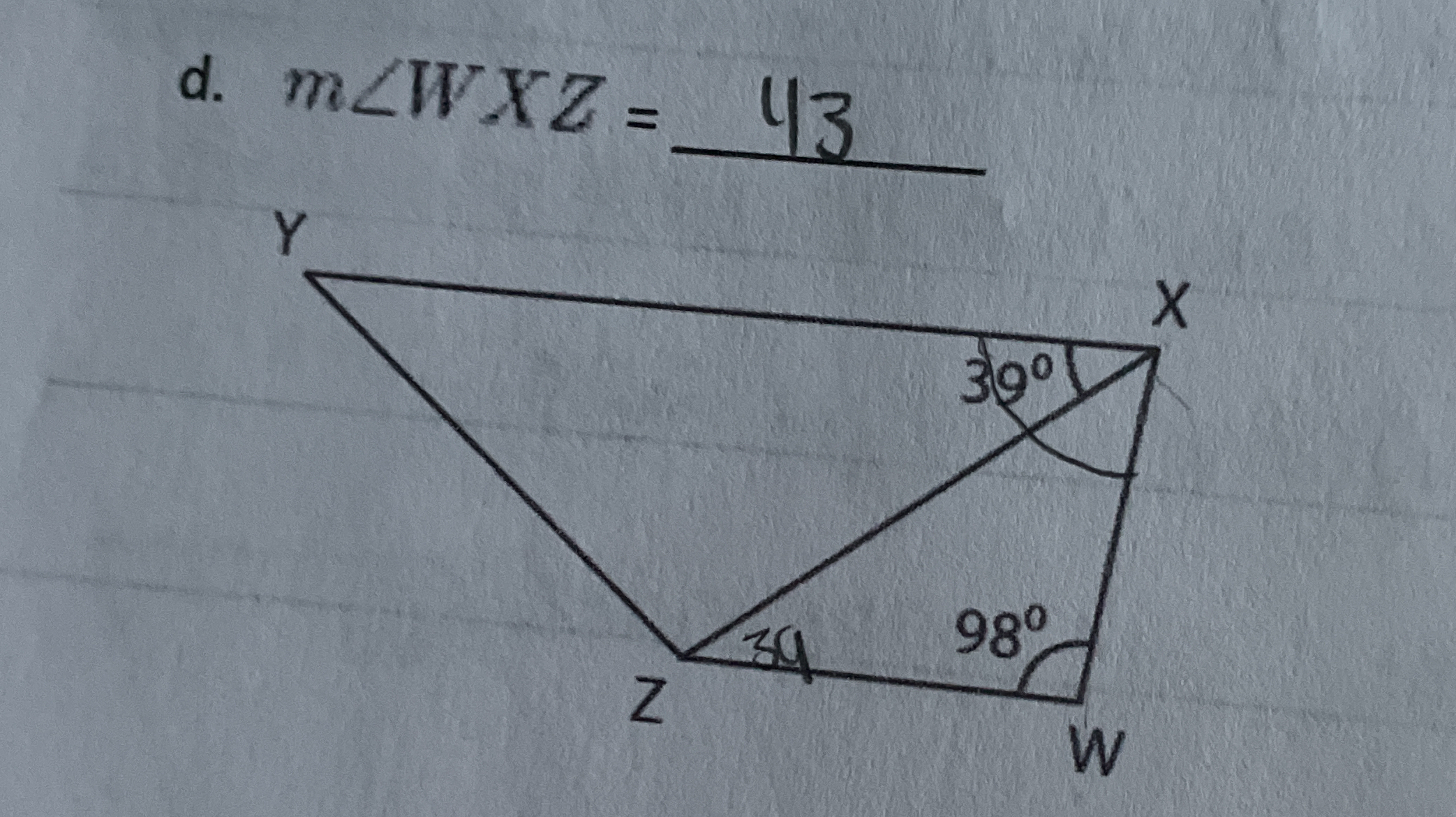
What is m∠WXZ if m∠YZX = 30° and m∠ZXY = 98°?
Understand the Problem
The question asks to find the measure of angle WXZ in a geometric figure, given certain angle measurements. It involves applying the concept of angle relationships.
Answer
The measure of angle $\angle WXZ$ is $52°$.
Answer for screen readers
The measure of angle $\angle WXZ$ is $52°$.
Steps to Solve
- Identify the Angles in the Figure
From the image, we have the following angle measurements:
- $m∠YWX = 30°$
- $m∠WXY = 98°$
- $m∠XYZ = 30°$
- Use the Triangle Angle Sum Property
In triangle $WXY$, the sum of the angles must equal $180°$. Therefore: $$ m∠WXY + m∠YWX + m∠WXZ = 180° $$
- Substitute Known Values Into the Equation
Now substitute the known angle values into the equation: $$ 98° + 30° + m∠WXZ = 180° $$
- Combine Like Terms
Add the known angles together: $$ 128° + m∠WXZ = 180° $$
- Isolate the Unknown Angle
To solve for $m∠WXZ$, subtract $128°$ from both sides: $$ m∠WXZ = 180° - 128° $$
- Calculate the Final Angle Measurement
Perform the calculation: $$ m∠WXZ = 52° $$
The measure of angle $\angle WXZ$ is $52°$.
More Information
In triangle geometry, the sum of angles is always $180°$. This property helps in finding unknown angles when you have the measures of the other angles.
Tips
- Forgetting that the sum of the angles in a triangle is $180°$.
- Misreading angles or incorrectly labeling them.
AI-generated content may contain errors. Please verify critical information