What is \( \frac{4}{5} + \frac{9}{6} \)?
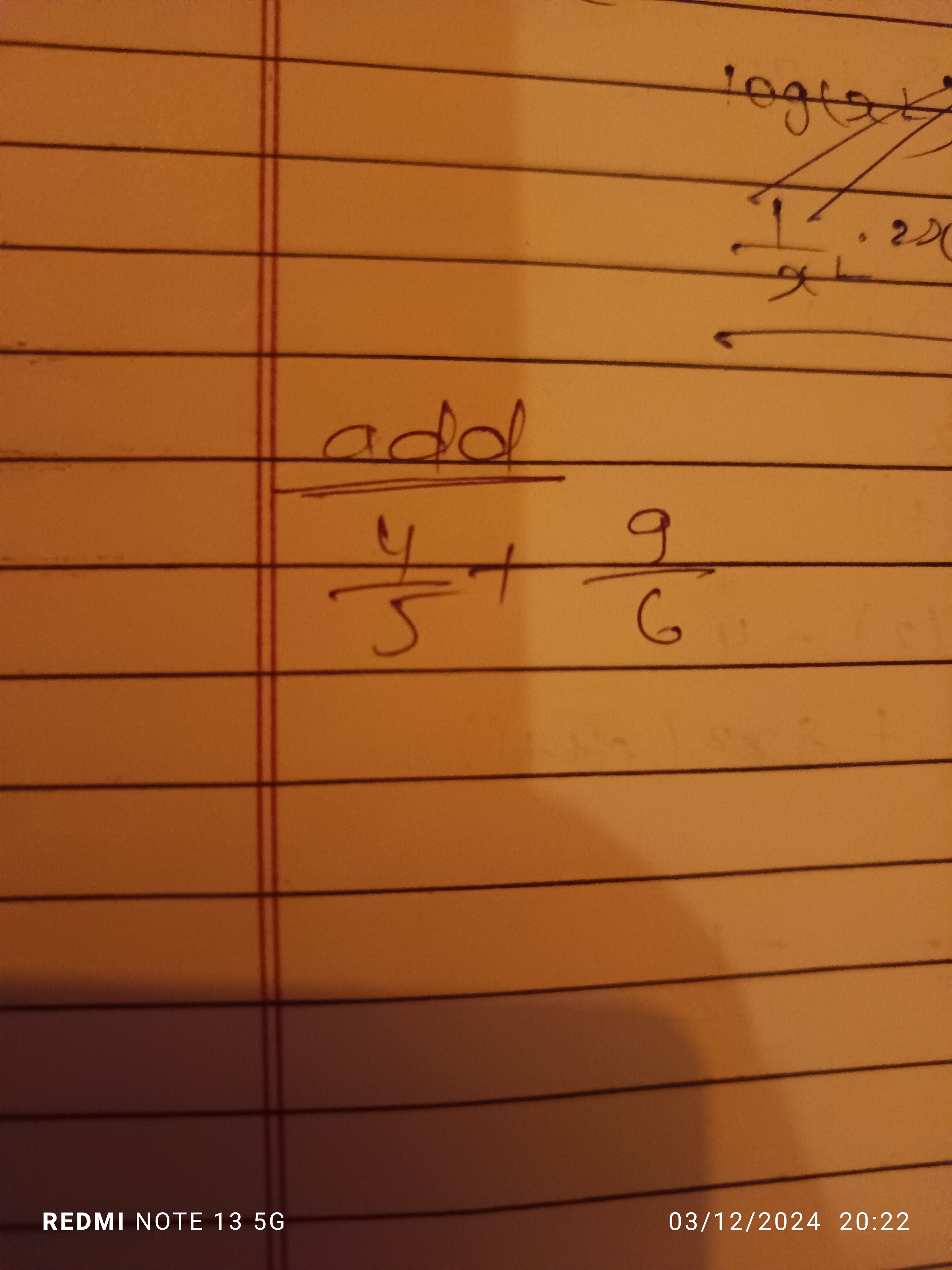
Understand the Problem
The question involves adding two fractions, specifically ( \frac{4}{5} + \frac{9}{6} ). The goal is to find a common denominator and compute the sum.
Answer
The answer is $\frac{69}{30}$ or $2 \frac{3}{10}$.
Answer for screen readers
The final answer is $\frac{69}{30}$ or $2 \frac{3}{10}$.
Steps to Solve
- Find the least common denominator (LCD)
To add the fractions $ \frac{4}{5} $ and $ \frac{9}{6} $, we first need to find the least common denominator. The denominators are 5 and 6. The least common multiple of 5 and 6 is 30.
- Convert the fractions to have the same denominator
Next, we convert each fraction to have the common denominator of 30.
For $ \frac{4}{5} $: $$ \frac{4}{5} = \frac{4 \times 6}{5 \times 6} = \frac{24}{30} $$
For $ \frac{9}{6} $: $$ \frac{9}{6} = \frac{9 \times 5}{6 \times 5} = \frac{45}{30} $$
- Add the two fractions
Now that both fractions have the same denominator, we can add them: $$ \frac{24}{30} + \frac{45}{30} = \frac{24 + 45}{30} = \frac{69}{30} $$
- Simplify if possible
Finally, we can check if the resulting fraction can be simplified. The fraction $ \frac{69}{30} $ can't be simplified further, but we can express it as a mixed number: $$ \frac{69}{30} = 2 \frac{9}{30} = 2 \frac{3}{10} $$
The final answer is $\frac{69}{30}$ or $2 \frac{3}{10}$.
More Information
When adding fractions, finding a common denominator is essential, and it helps in ensuring that the fractions are easily comparable. The process of simplifying fractions often leads to a more recognizable form.
Tips
- Forgetting to find a common denominator can lead to incorrect answers.
- Not simplifying the final fraction can leave the answer in a less optimal form.
AI-generated content may contain errors. Please verify critical information