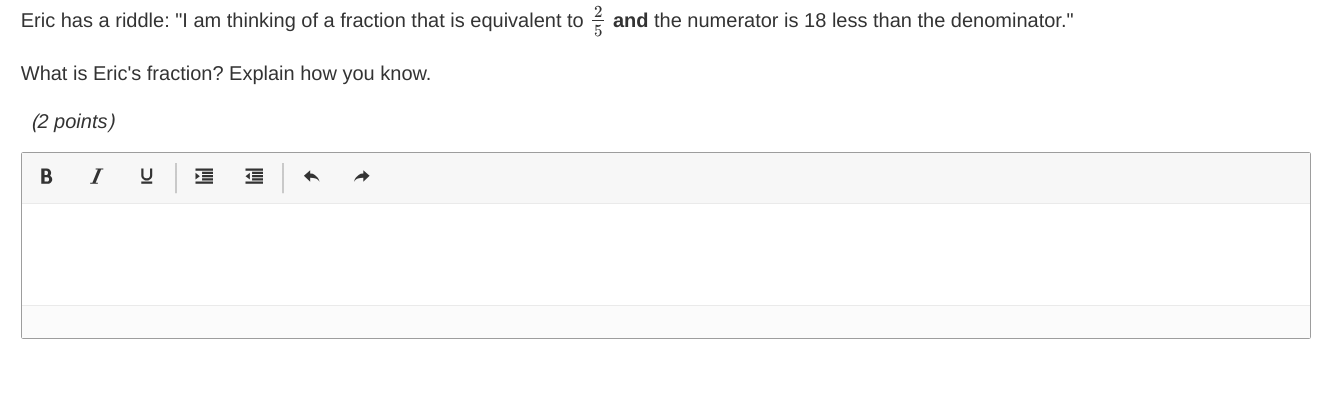
What is Eric's fraction? Explain how you know.

Steps to Solve

1. Define the variables

Let the denominator be ( d ). Then the numerator, according to the riddle, will be ( d - 18 ).

2. Set up the equation

Since we know that the fraction must be equivalent to ( \frac{2}{5} ), we can set up the equation:

$$ \frac{d - 18}{d} = \frac{2}{5} $$

3. Cross-multiply

To eliminate the fractions, we cross-multiply:

$$ 5(d - 18) = 2d $$

4. Simplify the equation

Now simplify the equation:

$$ 5d - 90 = 2d $$

Subtract ( 2d ) from both sides:

$$ 3d - 90 = 0 $$

5. Solve for ( d )

Add 90 to both sides:

$$ 3d = 90 $$

Now divide by 3:

$$ d = 30 $$

6. Find the numerator

Now substitute ( d ) back into the expression for the numerator:

$$ \text{Numerator} = d - 18 = 30 - 18 = 12 $$

7. Write the fraction

Therefore, Eric's fraction is:

$$ \frac{12}{30} $$

8. Simplify the fraction

Lastly, simplify ( \frac{12}{30} ):

$$ \frac{12 \div 6}{30 \div 6} = \frac{2}{5} $$