What choices of α, β, and γ does the function f(x) = { x^3, x ≤ 1; αx^2 + βx + γ, x > 1 } have for being twice differentiable at x = 1?
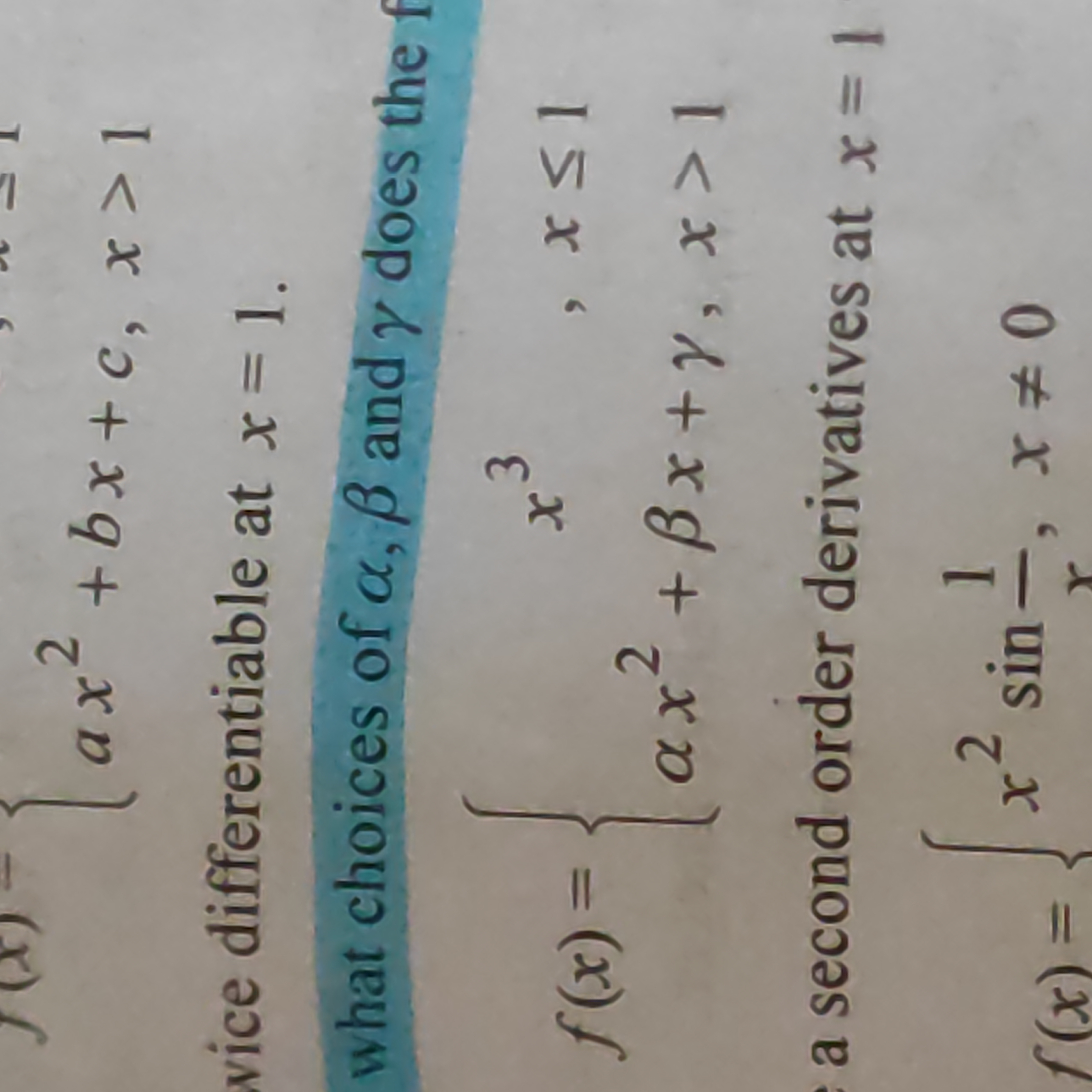
Understand the Problem
The question is asking to determine the values of parameters α, β, and γ in a piecewise function such that the function is twice differentiable at x = 1. This involves ensuring that both the function and its first and second derivatives are continuous at the point x = 1.
Answer
The values are $\alpha = 3$, $\beta = -3$, and $\gamma = 1$.
Answer for screen readers
The values are $\alpha = 3$, $\beta = -3$, and $\gamma = 1$.
Steps to Solve
- Set up the piecewise function and continuity requirements
The function is defined as:
$$ f(x) = \begin{cases} x^3, & x \leq 1 \ \alpha x^2 + \beta x + \gamma, & x > 1 \end{cases} $$
We want to ensure that $f(1)$ and its derivatives are continuous at $x = 1$.
- Ensure continuity of the function at x = 1
Set $f(1)$ from both parts equal to each other:
$$ 1^3 = \alpha(1^2) + \beta(1) + \gamma $$
which simplifies to:
$$ 1 = \alpha + \beta + \gamma \tag{1} $$
- Ensure continuity of the first derivative at x = 1
Calculate the derivatives:
$$ f'(x) = \begin{cases} 3x^2, & x < 1 \ 2\alpha x + \beta, & x > 1 \end{cases} $$
Evaluate the derivatives at $x = 1$:
$$ f'(1^-) = 3(1^2) = 3 $$
Set the two derivatives equal:
$$ 3 = 2\alpha(1) + \beta \tag{2} $$
- Ensure continuity of the second derivative at x = 1
Calculate the second derivatives:
$$ f''(x) = \begin{cases} 6x, & x < 1 \ 2\alpha, & x > 1 \end{cases} $$
Evaluate at $x = 1$:
$$ f''(1^-) = 6(1) = 6 $$
Set them equal:
$$ 6 = 2\alpha \tag{3} $$
- Solve the equations simultaneously
From equation (3), solve for $\alpha$:
$$ \alpha = 3 $$
Substitute $\alpha$ into equation (2):
$$ 3 = 2(3) + \beta \implies 3 = 6 + \beta \implies \beta = -3 $$
Now substitute $\alpha$ and $\beta$ into equation (1):
$$ 1 = 3 - 3 + \gamma \implies \gamma = 1 $$
- Final values for parameters
The values are:
- $\alpha = 3$
- $\beta = -3$
- $\gamma = 1$
The values are $\alpha = 3$, $\beta = -3$, and $\gamma = 1$.
More Information
These values ensure that the piecewise function is continuous and has continuous first and second derivatives at $x = 1$.
Tips
- Forgetting to set up equations for both the first and second derivative continuity.
- Neglecting to simplify equations properly.
- Confusing the continuity requirements for derivatives at the transition point.
AI-generated content may contain errors. Please verify critical information