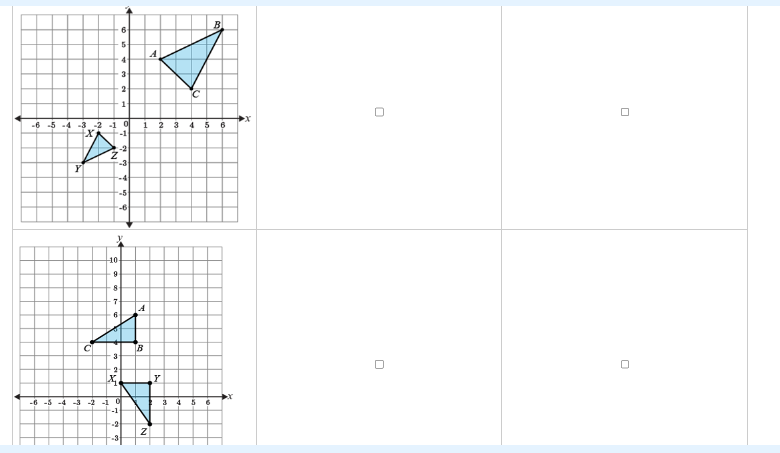
What are the properties or transformations of the triangles shown in the coordinate planes?
Understand the Problem
The question appears to be related to geometry and transformations involving figures plotted on a coordinate plane. It likely asks about properties or operations related to the triangles shown in the images.
Answer
The triangles are related by a reflection across the x-axis.
Answer for screen readers
The triangles are related by a reflection across the x-axis.
Steps to Solve
-
Identify the Coordinates of the Triangles First, determine the coordinates of the points for both triangles. For the upper triangle, let the coordinates be:
- A(1, 3)
- B(4, 5)
- C(2, 1)
For the lower triangle, the coordinates are:
- A(1, -3)
- B(-4, -5)
- C(-2, -1)
-
Determine if Transformations Occurred Analyze the transformations from the upper triangle to the lower triangle. Note that the triangles appear to be reflections.
The transformation can be described as flipping across the x-axis.
-
Express the Transformation Algebraically To obtain the coordinates of the lower triangle from the upper triangle, reflect each point A, B, and C across the x-axis:
- For point A: (x, y) will become (x, -y)
- For point B: (4, 5) becomes (4, -5)
- For point C: (2, 1) becomes (2, -1)
-
Write Down the New Points After Transformation The new points after reflection across the x-axis are:
- A'(1, -3)
- B'(4, -5)
- C'(2, -1)
The triangles are related by a reflection across the x-axis.
More Information
This transformation shows that geometric figures can be transformed through reflections, maintaining their shape while altering their position.
Tips
- Incorrectly identifying the transformation: Ensure to carefully analyze the orientation of the triangles before concluding the type of transformation.
- Forgetting to apply the transformation to all points: Make sure to consistently apply the transformation rule to each point of the triangle.
AI-generated content may contain errors. Please verify critical information