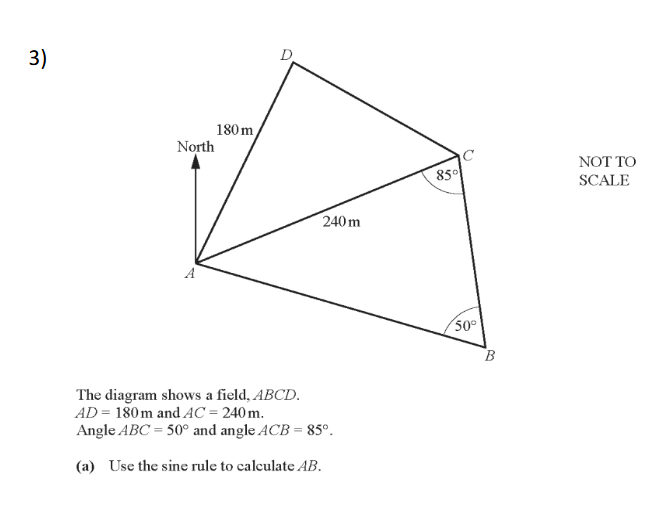
Use the sine rule to calculate AB.

Steps to Solve

1. Identify the angles and sides In triangle ABC:

• Given:
  • $AD = 180,m$
  • $AC = 240,m$
  • Angle $ABC = 50^\circ$
  • Angle $ACB = 85^\circ$

2. Calculate the missing angle To find angle $CAB$, use the fact that the sum of angles in a triangle is $180^\circ$: $$ \text{Angle } CAB = 180^\circ - \text{Angle } ABC - \text{Angle } ACB $$ Substituting the known values: $$ CAB = 180^\circ - 50^\circ - 85^\circ $$

3. Calculate angle CAB Now we calculate: $$ CAB = 180^\circ - 135^\circ = 45^\circ $$

4. Apply the Sine Rule According to the sine rule: $$ \frac{AB}{\sin(CAB)} = \frac{AC}{\sin(ABC)} $$ Rearranging this gives: $$ AB = \frac{AC \cdot \sin(CAB)}{\sin(ABC)} $$

5. Substitute the known values Now substitute:

• $AC = 240,m$
• $\sin(CAB) = \sin(45^\circ)$
• $\sin(ABC) = \sin(50^\circ)$

This gives: $$ AB = \frac{240 \cdot \sin(45^\circ)}{\sin(50^\circ)} $$

6. Calculate the sine values Using the values:

• $\sin(45^\circ) \approx 0.7071$
• $\sin(50^\circ) \approx 0.7660$

7. Final calculation Substituting these values in: $$ AB = \frac{240 \cdot 0.7071}{0.7660} $$ Calculating this yields: $$ AB \approx 221.66,m $$