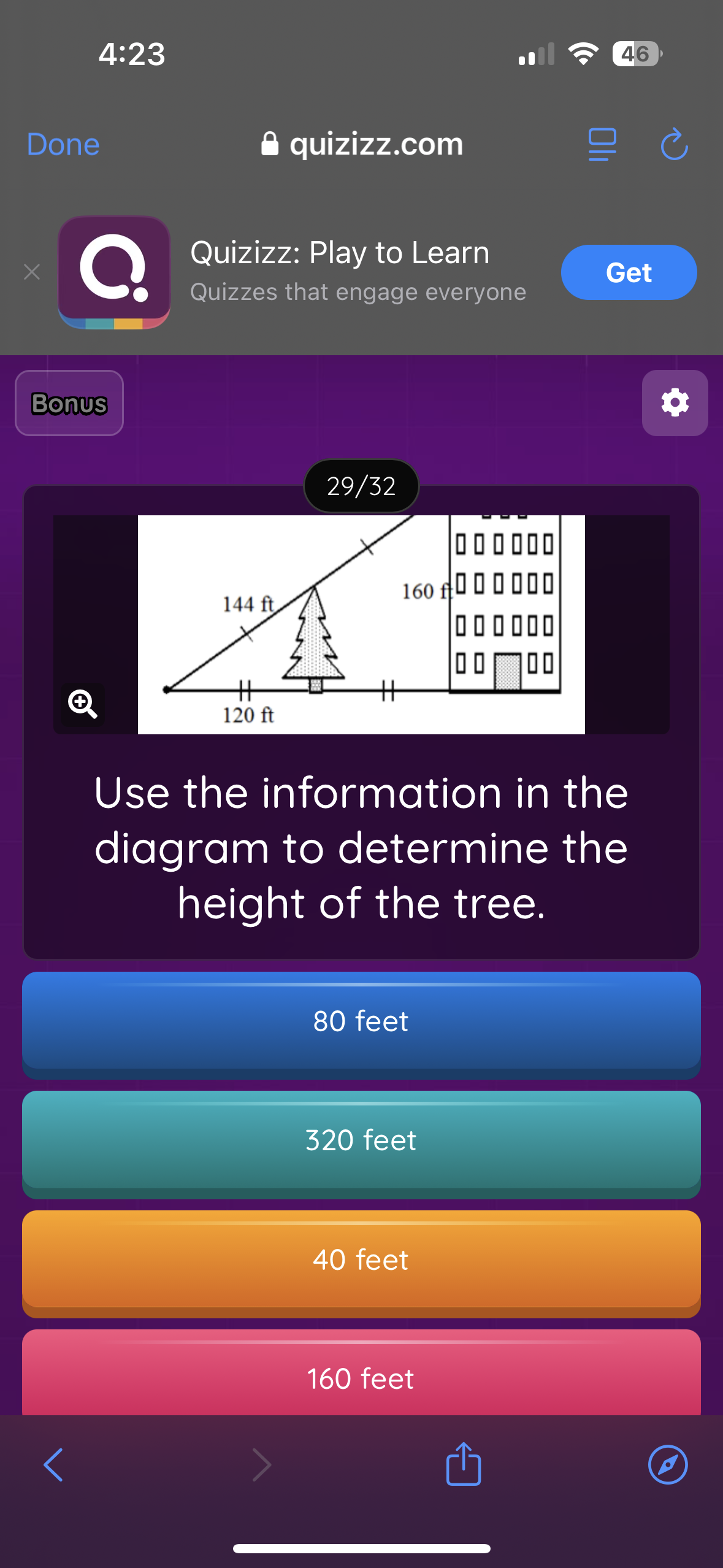
Use the information in the diagram to determine the height of the tree.

Steps to Solve

1. Understand the Geometry
   The problem involves a right triangle, where the height of the tree represents one leg, the distance from the observer (120 ft) is the base, and the hypotenuse is represented by the line from the top of the tree to the observer. The hypotenuse measures 144 ft.

2. Apply the Pythagorean Theorem
   Use the Pythagorean theorem, which states that for a right triangle:
   $$ a^2 + b^2 = c^2 $$
   Here, $a$ is the height of the tree (unknown), $b$ is the distance from the observer (120 ft), and $c$ is the length of the hypotenuse (144 ft). So the equation becomes:
   $$ h^2 + 120^2 = 144^2 $$

3. Calculate the Squares
   Calculate the squares:
   $$ 120^2 = 14400 $$
   $$ 144^2 = 20736 $$

4. Set Up the Equation
   Substituting the square values into the equation:
   $$ h^2 + 14400 = 20736 $$

5. Solve for Height
   Isolate $h^2$ by subtracting 14400 from both sides:
   $$ h^2 = 20736 - 14400 $$
   Calculate the result:
   $$ h^2 = 6336 $$

6. Find the Height
   Take the square root of both sides to find $h$:
   $$ h = \sqrt{6336} $$
   Calculate the square root to find the height.