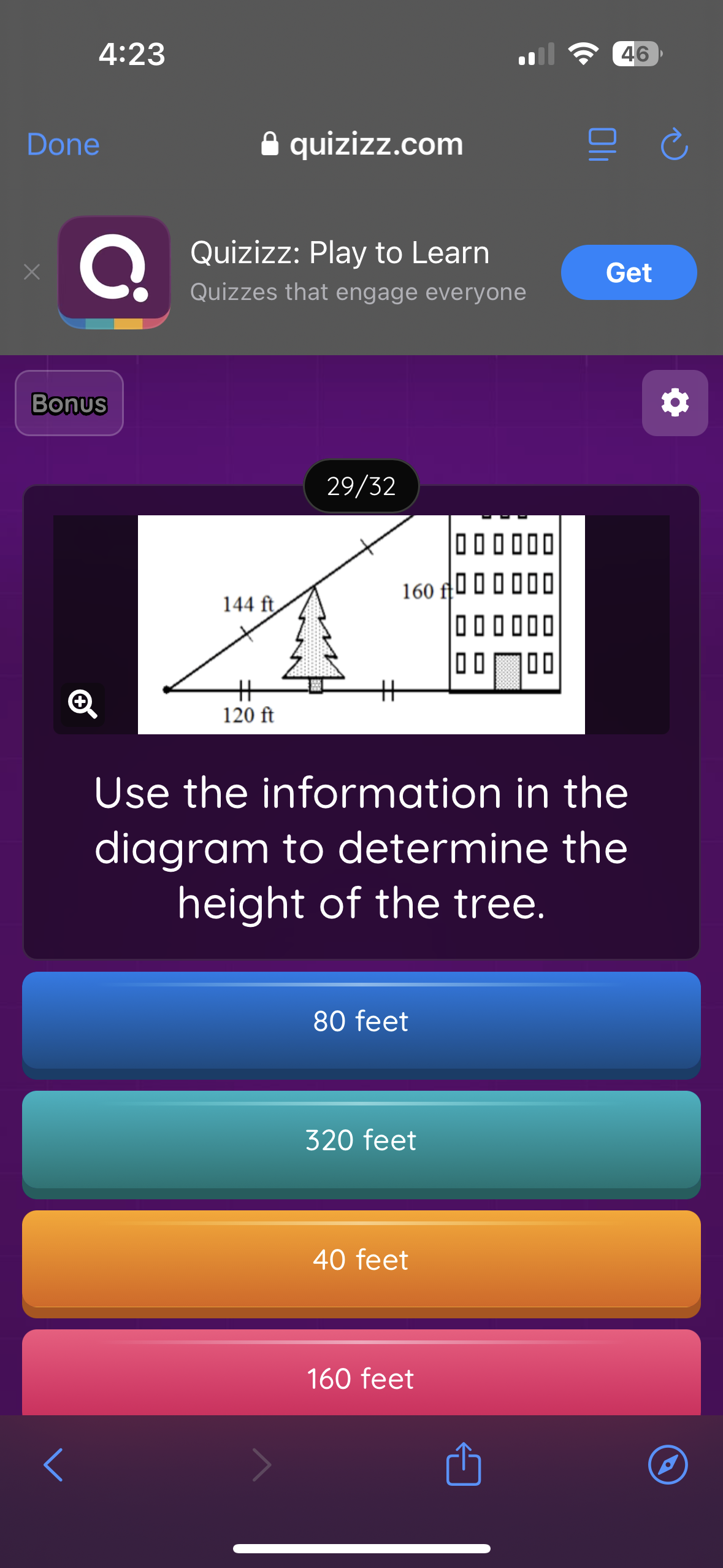
Use the information in the diagram to determine the height of the tree.

Steps to Solve

1. Identify the triangle and its components

The right triangle is formed by the height of the tree (let's call it $h$), the horizontal ground distance of 120 ft, and the slant height of 144 ft.

2. Apply the Pythagorean theorem

We can use the Pythagorean theorem, which states that in a right triangle:

$$ a^2 + b^2 = c^2 $$

where $a$ and $b$ are the lengths of the legs, and $c$ is the length of the hypotenuse. Here:

• $a = 120$ ft (horizontal distance)
• $c = 144$ ft (slant height)

We need to find the height $h$, which is the other leg of the triangle.

3. Set up the equation

Using the Pythagorean theorem:

$$ 120^2 + h^2 = 144^2 $$

4. Calculate the squares

Compute the squares of each value:

• $120^2 = 14400$
• $144^2 = 20736$

5. Create the equation for $h$

Now plug in the values:

$$ 14400 + h^2 = 20736 $$

6. Solve for $h^2$

Rearranging gives:

$$ h^2 = 20736 - 14400 $$

Calculating this:

$$ h^2 = 6336 $$

7. Find the height $h$ by taking the square root

Take the square root of both sides:

$$ h = \sqrt{6336} $$

Calculating the square root:

$$ h \approx 79.6 $$

Thus, we can round the answer to 80 feet.