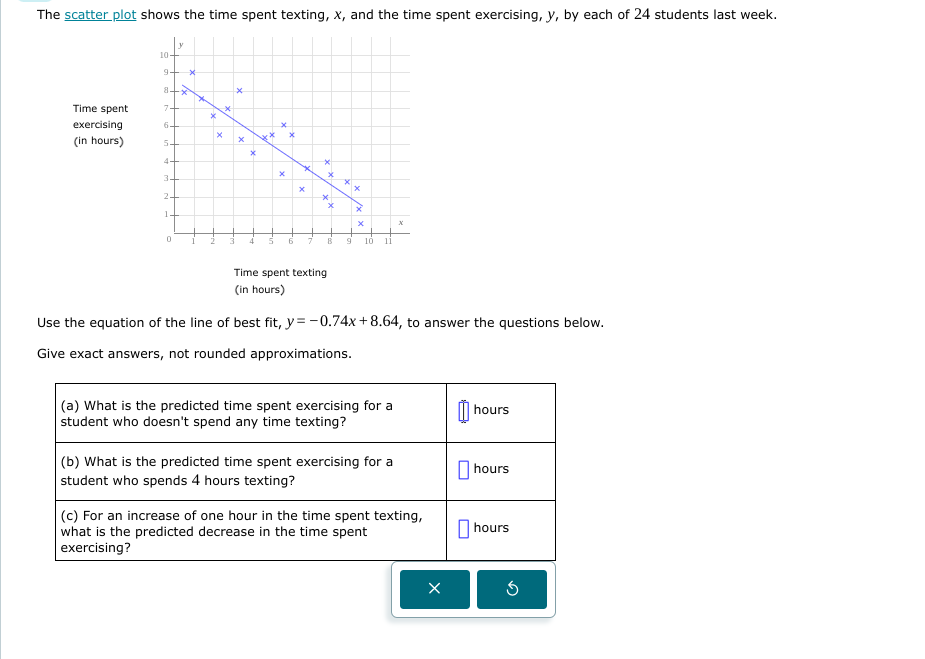
Use the equation of the line of best fit, y = -0.74x + 8.64, to answer the questions below. (a) What is the predicted time spent exercising for a student who doesn't spend any time... Use the equation of the line of best fit, y = -0.74x + 8.64, to answer the questions below. (a) What is the predicted time spent exercising for a student who doesn't spend any time texting? (b) What is the predicted time spent exercising for a student who spends 4 hours texting? (c) For an increase of one hour in the time spent texting, what is the predicted decrease in the time spent exercising?
Understand the Problem
The question is asking for predictions based on a linear regression equation from a scatter plot that represents the relationship between time spent texting and time spent exercising. It requires the use of the equation of the line of best fit to answer three specific questions regarding time predictions and changes.
Answer
(a) 8.64 hours (b) 5.68 hours (c) 0.74 hours
Answer for screen readers
(a) 8.64 hours
(b) 5.68 hours
(c) 0.74 hours
Steps to Solve
- Understanding the equation of the line
The line of best fit is given by the equation:
$$ y = -0.74x + 8.64 $$
where ( y ) represents the time spent exercising, and ( x ) represents the time spent texting.
- Calculating for part (a)
To find the predicted exercise time for a student who doesn't spend any time texting, substitute ( x = 0 ) into the equation:
$$ y = -0.74(0) + 8.64 = 8.64 $$
- Calculating for part (b)
For a student who spends 4 hours texting, substitute ( x = 4 ):
$$ y = -0.74(4) + 8.64 $$
Calculating gives:
$$ y = -2.96 + 8.64 = 5.68 $$
- Calculating for part (c)
The slope of the line, ( -0.74 ), indicates the predicted decrease in time spent exercising for each additional hour spent texting. Thus, the change in exercise time for an increase of 1 hour in texting is:
$$ \text{Decrease} = -0.74 $$
(a) 8.64 hours
(b) 5.68 hours
(c) 0.74 hours
More Information
The equation ( y = -0.74x + 8.64 ) illustrates a negative correlation between time spent texting and time spent exercising, meaning that as one increases, the other decreases.
Tips
- Misinterpreting the slope: Remember that the slope represents the change in ( y ) per unit change in ( x ). In this case, it's a decrease for an increase in texting time.
- Not substituting correctly into the equation: Ensure to accurately substitute the given values for ( x ) into the equation.
AI-generated content may contain errors. Please verify critical information