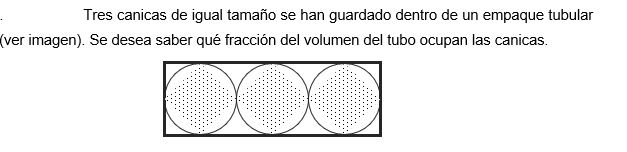
Tres canicas de igual tamaño se han guardado dentro de un empaque tubular. Se desea saber qué fracción del volumen del tubo ocupan las canicas.

Steps to Solve

1. Calcular el volumen de una canica

El volumen de una esfera se calcula con la fórmula:

$$ V = \frac{4}{3} \pi r^3 $$

donde $r$ es el radio de la canica. Si el radio de cada canica es $r$, entonces el volumen de tres canicas es:

$$ V_{\text{total}} = 3 \times \frac{4}{3} \pi r^3 = 4 \pi r^3 $$

2. Calcular el volumen del tubo

Suponiendo que el tubo tiene un diámetro igual al de tres canicas alineadas, el diámetro total del tubo (D) sería el triple del diámetro de una canica (d):

$$ D = 3d = 6r $$

El volumen de un cilindro se calcula con:

$$ V = \pi R^2 h $$

donde $R$ es el radio del tubo y $h$ es la altura (o longitud) del tubo. Así que:

$$ V_{\text{tubo}} = \pi \left(\frac{D}{2}\right)^2 h = \pi \left(3r\right)^2 h = 9 \pi r^2 h $$

3. Calcular la fracción del volumen ocupado por las canicas

La fracción del volumen del tubo que ocupan las canicas se calcula como:

$$ \text{fracción} = \frac{V_{\text{canicas}}}{V_{\text{tubo}}} = \frac{4 \pi r^3}{9 \pi r^2 h} $$

Simplificando:

$$ \text{fracción} = \frac{4r}{9h} $$

Esto nos da la fracción del volumen del tubo que está ocupada por las canicas.