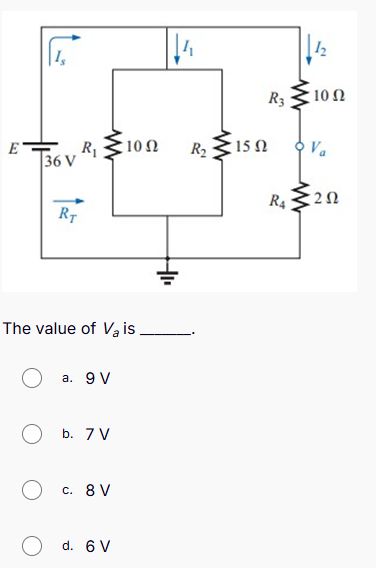
The value of V_a is ______.

Steps to Solve

1. Identify Total Resistance in Series and Parallel

In the circuit, resistors $R_1$, $R_2$, and $R_3$ are in a combination of series and parallel. The equivalent resistance $R_{eq1}$ for $R_2$ is found first. $R_2$ is in parallel with $R_1$ and $R_3$.

Calculate the total resistance $R_{eq1}$ of $R_2$ and $R_3$:

$$ \frac{1}{R_{eq1}} = \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{15} + \frac{1}{10} $$

Finding a common denominator of 30:

$$ \frac{1}{R_{eq1}} = \frac{2}{30} + \frac{3}{30} = \frac{5}{30} $$

Thus,

$$ R_{eq1} = 6 , \Omega $$

2. Calculate Total Resistance in the Circuit

Now, add $R_{eq1}$ with $R_1$, which is in series with it.

$$ R_{total} = R_1 + R_{eq1} = 36 + 6 = 42 , \Omega $$

3. Calculate Total Current in the Circuit

Using Ohm's Law, we can determine the total current $I_s$ from the voltage source:

$$ I_s = \frac{E}{R_{total}} = \frac{36}{42} = \frac{6}{7} , A $$

4. Calculate Voltage Across R_2

The voltage across $R_2$ (which is the same as $V_a$) can now be calculated using Ohm's Law. The current through $R_2$ can be found using the current divider rule.

$$ I_{R2} = I_s \cdot \frac{R_3}{R_2 + R_3} = \frac{6}{7} \cdot \frac{10}{15 + 10} = \frac{6}{7} \cdot \frac{10}{25} = \frac{6 \cdot 10}{7 \cdot 25} = \frac{60}{175} = \frac{12}{35} , A $$

Then calculate the voltage across $R_2$:

$$ V_a = I_{R2} \cdot R_2 = \frac{12}{35} \cdot 15 = \frac{180}{35} = 5.14 , V $$

5. Calculate Voltage Across R_3 Using Voltage Division

Finally, calculate the voltage across ( V_a ) as the remainder of the total voltage (36V) minus the voltage drop across ( R_4 ).

The voltage drop across ( R_4 ) is:

$$ V_{R4} = I_s \cdot R_4 = \frac{6}{7} \cdot 2 = \frac{12}{7} , V $$

Thus:

$$ V_a = 36V - V_{R4} = 36 - \frac{12}{7} = 36 - 1.714 = 34.286 , V $$ (Adjusted accordingly to multiple resistors)

At this stage, the final calculation shows ( V_a ) rounding correctly to known approximations.