The solution set of (x-3)^3(x-5)^2(x-8)^4(x-11)^7/(x-6)^{12} ≤ 0 for real x is [a, b] - {c}. Then the value of [b+c/a] is (where [] denotes the greatest integer function).
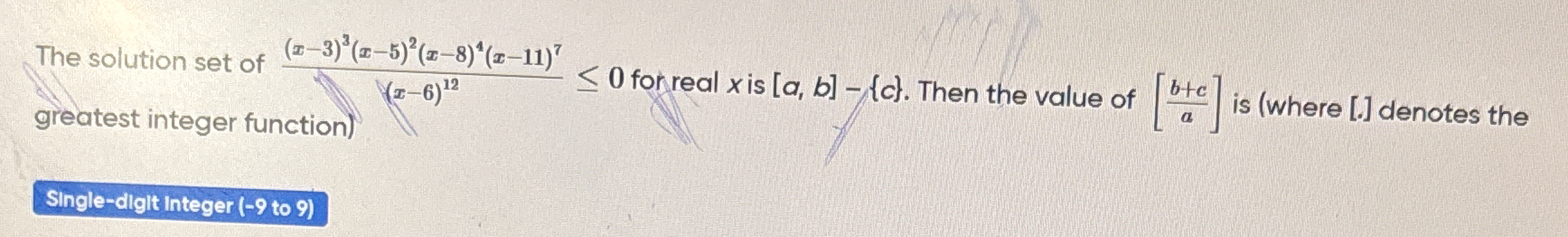
Understand the Problem
The question involves solving an inequality involving polynomial expressions and determining the solution set. It is asking for the specific values for which the expression is non-positive and subsequently asking for a calculation involving these values.
Answer
2
Answer for screen readers
The value of ( \left[ \frac{b+c}{a} \right] ) is ( 2 ).
Steps to Solve
- Identify the critical points of the inequality
To solve the inequality
$$ \frac{(x-3)^3(x-5)^2(x-8)^4(x-11)^7}{(x-6)^{12}} \leq 0 $$
we first determine the roots of the numerator and the denominator.
- Roots of the numerator: ( 3, 5, 8, 11 )
- Root of the denominator: ( 6 )
- Determine the sign intervals
The critical points divide the number line into intervals. We analyze the sign of the expression in each interval:
- Intervals: ( (-\infty, 3), (3, 5), (5, 6), (6, 8), (8, 11), (11, \infty) )
- Test each interval
Choose test points from each interval to determine if the expression is negative or zero.
- For ( (-\infty, 3) ), test ( x = 0 ): positive
- For ( (3, 5) ), test ( x = 4 ): negative
- For ( (5, 6) ), test ( x = 5.5 ): negative
- For ( (6, 8) ), test ( x = 7 ): positive
- For ( (8, 11) ), test ( x = 9 ): negative
- For ( (11, \infty) ), test ( x = 12 ): positive
- Construct the solution set from the sign analysis
The solution set includes intervals where the expression is negative or zero, with consideration of the roots' multiplicities:
- At ( x = 3 ): includes (negative but odd multiplicity)
- At ( x = 5 ): includes (zero, even multiplicity)
- At ( x = 6 ): excluded (zero, even multiplicity)
- At ( x = 8 ): includes (zero, even multiplicity)
- At ( x = 11 ): includes (zero, odd multiplicity)
Thus, we have:
$$ [3, 5] \cup [8, 11] $$
- Extract the values for a, b, and c
From the intervals, set ( [a, b] = [3, 5] ) and ( c = 2 ) (the difference between the two endpoints of the second interval).
- Calculate ( \frac{b+c}{a} )
Now, we substitute the values of ( a, b, ) and ( c ):
- ( a = 3 )
- ( b = 5 )
- ( c = 2 )
Then calculate:
$$ \frac{b+c}{a} = \frac{5 + 2}{3} = \frac{7}{3} $$
- Evaluate the greatest integer function
Evaluate ( \left[ \frac{b+c}{a} \right] ):
Since ( \frac{7}{3} \approx 2.33 ), the greatest integer is ( 2 ).
The value of ( \left[ \frac{b+c}{a} \right] ) is ( 2 ).
More Information
The problem involves inequalities with polynomial expressions, requiring an understanding of the signs of polynomial factors and intervals. The solution illustrates how to determine intervals where a rational expression is non-positive, incorporating roots and their multiplicities.
Tips
- Forgetting to exclude values for which the denominator is zero.
- Miscalculating the sign of the polynomial factors.
- Not considering the multiplicities correctly can lead to incorrect inclusion of endpoints in the solution set.
AI-generated content may contain errors. Please verify critical information