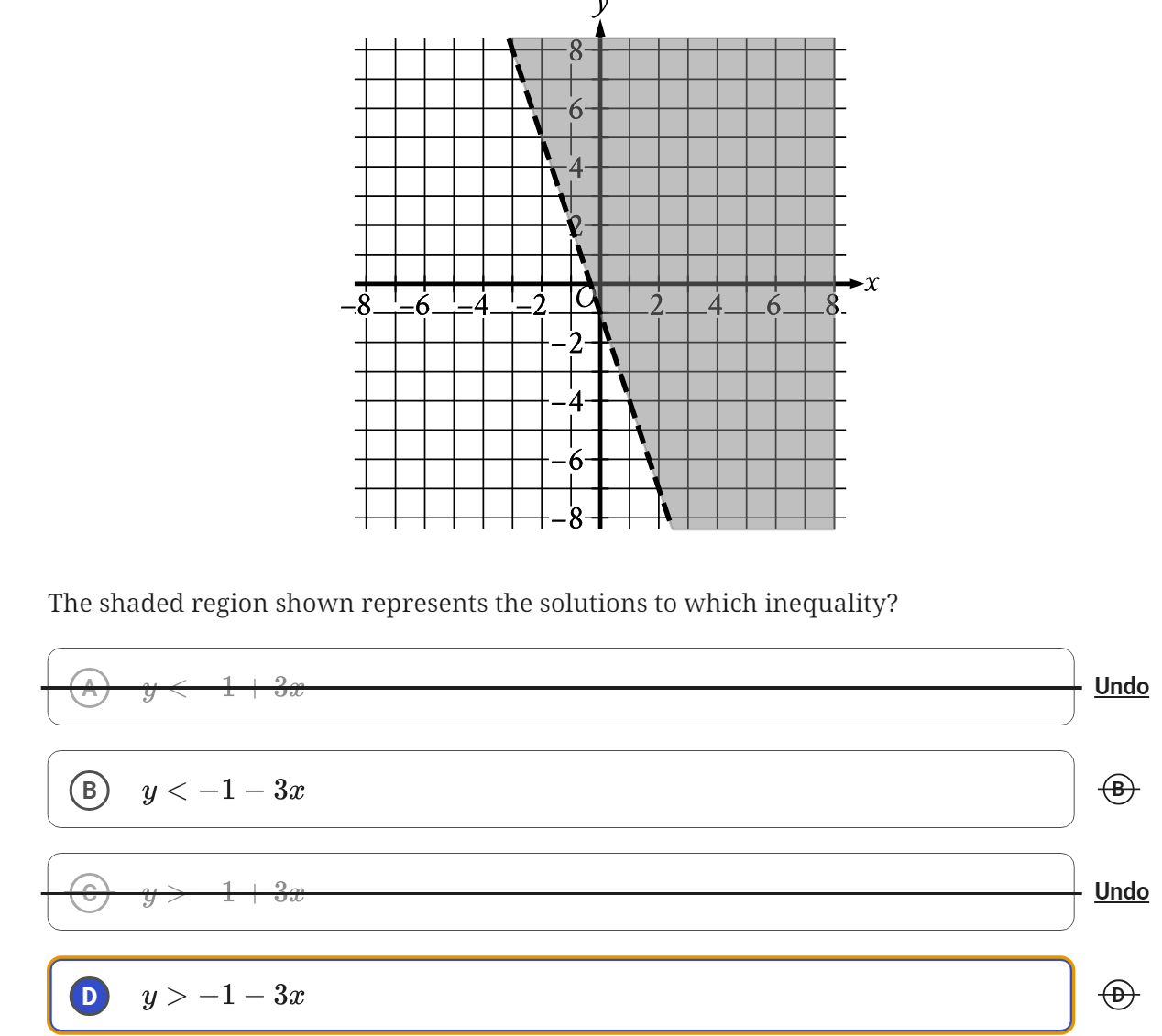
The shaded region shown represents the solutions to which inequality?
Understand the Problem
The question is asking which inequality corresponds to the shaded region in the provided graph. To determine the correct inequality, one must identify the boundary line and the region that it defines.
Answer
The inequality is \( y < -1 - 3x \).
Answer for screen readers
The inequality corresponding to the shaded region is ( y < -1 - 3x ).
Steps to Solve
-
Identify the boundary line The boundary line in the graph can be identified by its slope and y-intercept. The line appears to have a negative slope and crosses the y-axis at $y = -1$.
-
Determine the slope From the graph, the line seems to decrease as $x$ increases. If the line passes through points like $(0, -1)$ and $(1, -4)$, we can calculate the slope using the formula: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-4 - (-1)}{1 - 0} = \frac{-3}{1} = -3 $$
-
Form the equation of the line Using the slope-intercept form $y = mx + b$, substitute $m = -3$ and $b = -1$: $$ y = -3x - 1 $$
-
Identify the shaded region's inequality The shaded region is below the line, so we need to use a "less than" inequality. Hence, the inequality corresponding to the line is: $$ y < -3x - 1 $$
This matches option B, which is also frequently represented as $y < -1 - 3x$.
The inequality corresponding to the shaded region is ( y < -1 - 3x ).
More Information
The boundary line's equation helps define where the solutions (shaded region) lie in relation to the line. Since the shaded region is below the line, we use the less than inequality.
Tips
null
AI-generated content may contain errors. Please verify critical information