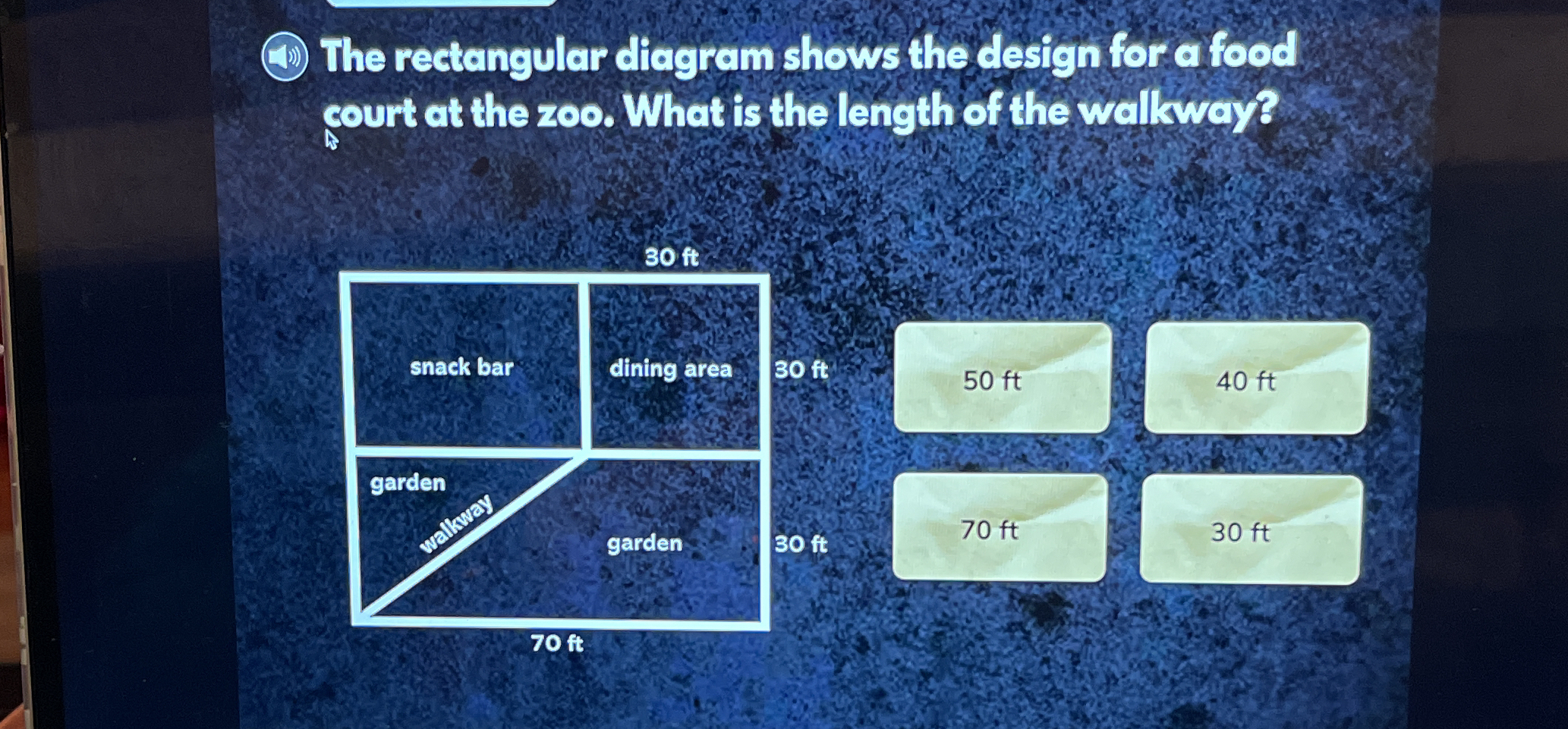
The rectangular diagram shows the design for a food court at the zoo. What is the length of the walkway?
Understand the Problem
The question presents a diagram of a food court design at a zoo and asks us to determine the length of the walkway. To do this, we can use the Pythagorean theorem, since the walkway forms the hypotenuse of a right triangle.
Answer
50 ft
Answer for screen readers
50 ft
Steps to Solve
- Identify the sides of the right triangle
The sides of the right triangle are the base and the height. The base is $70 - 30 = 40$ ft. The height is $30$ ft.
- Apply the Pythagorean theorem
The Pythagorean theorem states that $a^2 + b^2 = c^2$, where $a$ and $b$ are the lengths of the two shorter sides of a right triangle, and $c$ is the length of the hypotenuse.
In this case, $a = 40$ and $b = 30$, and we need to find $c$.
$$c = \sqrt{a^2 + b^2}$$
$$c = \sqrt{40^2 + 30^2}$$
- Calculate $c$
$$c = \sqrt{1600 + 900}$$
$$c = \sqrt{2500}$$
$$c = 50$$
The length of the walkway is 50 ft.
50 ft
More Information
The Pythagorean theorem is a fundamental concept in geometry related to the relationship between the sides of a right triangle. It has many applications in various fields, including architecture, engineering, and navigation.
Tips
A common mistake is to use the full length of the rectangle's sides instead of calculating the actual lengths of the triangle sides. Another mistake would be to add the sides before squaring them. You must square the sides, add them together, and then take the square root.
AI-generated content may contain errors. Please verify critical information