The graph of f(x) = 2x^4 - x^3 + 4x^2 - x + 2 has at most how many zeros?
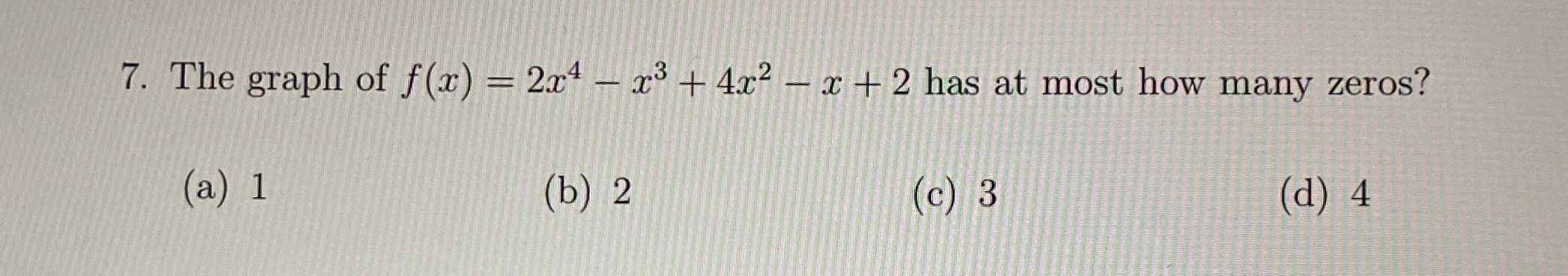
Understand the Problem
The question is asking how many zeros (roots) the polynomial function can have at most. The function provided is a polynomial of degree 4, and the question is looking for the maximum number of real zeros it can have.
Answer
The polynomial has at most 4 zeros.
Answer for screen readers
The graph of ( f(x) = 2x^4 - x^3 + 4x^2 - x + 2 ) has at most 4 zeros.
Steps to Solve
- Identify the Degree of the Polynomial
The given polynomial function is ( f(x) = 2x^4 - x^3 + 4x^2 - x + 2 ), which is a polynomial of degree 4. The degree of a polynomial indicates the highest exponent of ( x ) in the function.
- Determine the Maximum Number of Real Zeros
The maximum number of real zeros (roots) a polynomial can have is equal to its degree. Since the degree is 4, the polynomial can have at most 4 real zeros.
- Conclusion
Thus, the answer is based solely on the degree of the polynomial, which tells us the maximum possible number of intersections with the x-axis.
The graph of ( f(x) = 2x^4 - x^3 + 4x^2 - x + 2 ) has at most 4 zeros.
More Information
Polynomials of degree ( n ) can have up to ( n ) real roots, although not all of them may be distinct or real. In this case, the highest degree (4) allows for up to 4 intersections with the x-axis.
Tips
- Ignoring complex roots: While a degree 4 polynomial can have up to 4 real zeros, some may be complex; ensure not to confuse total roots with real roots.
- Miscounting intersections: Sometimes, it’s assumed that all degrees equate to distinct real zeros without graphical evaluation.
AI-generated content may contain errors. Please verify critical information