The domain of the function f(x) = √(x + 2)/(x - 4) is
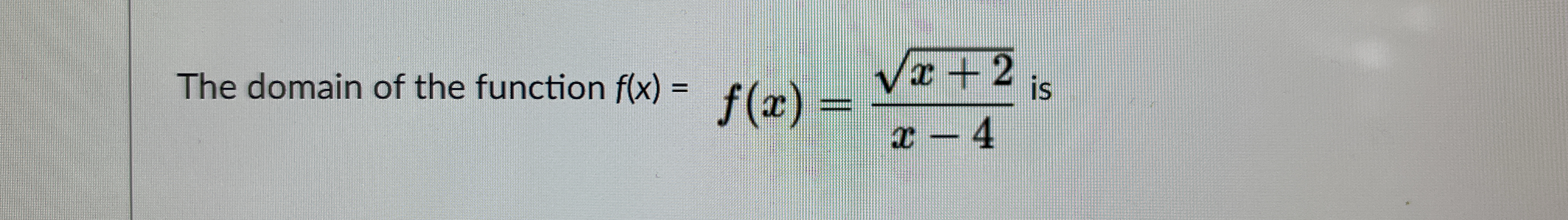
Understand the Problem
The question is asking for the domain of the given function, which involves determining the values of x that make the function valid.
Answer
The domain of the function is \( x \in [-2, 4) \cup (4, \infty) \).
Answer for screen readers
The domain of the function is ( x \in [-2, 4) \cup (4, \infty) ).
Steps to Solve
-
Identify conditions for the square root The expression under the square root must be non-negative: $$ x + 2 \geq 0 $$
-
Solve the inequality To find the values of $x$, subtract 2 from both sides: $$ x \geq -2 $$
-
Identify conditions for the denominator The denominator cannot be zero: $$ x - 4 \neq 0 $$
-
Solve the equation for the denominator Set the denominator equal to zero and solve: $$ x - 4 = 0 \implies x \neq 4 $$
-
Combine the conditions The domain must satisfy both conditions:
- From the square root, we have $x \geq -2$.
- From the denominator, $x \neq 4$.
Thus, the domain of the function is: $$ x \in [-2, 4) \cup (4, \infty) $$
The domain of the function is ( x \in [-2, 4) \cup (4, \infty) ).
More Information
This domain includes all real numbers greater than or equal to -2 except for the value 4, where the function is undefined due to the zero in the denominator. Understanding these restrictions allows for the proper usage of the function in calculations.
Tips
- Ignoring the square root condition: Always check that the expression inside the square root is non-negative.
- Forgetting about the denominator: It’s crucial to ensure that you do not include values that make the denominator zero.
AI-generated content may contain errors. Please verify critical information