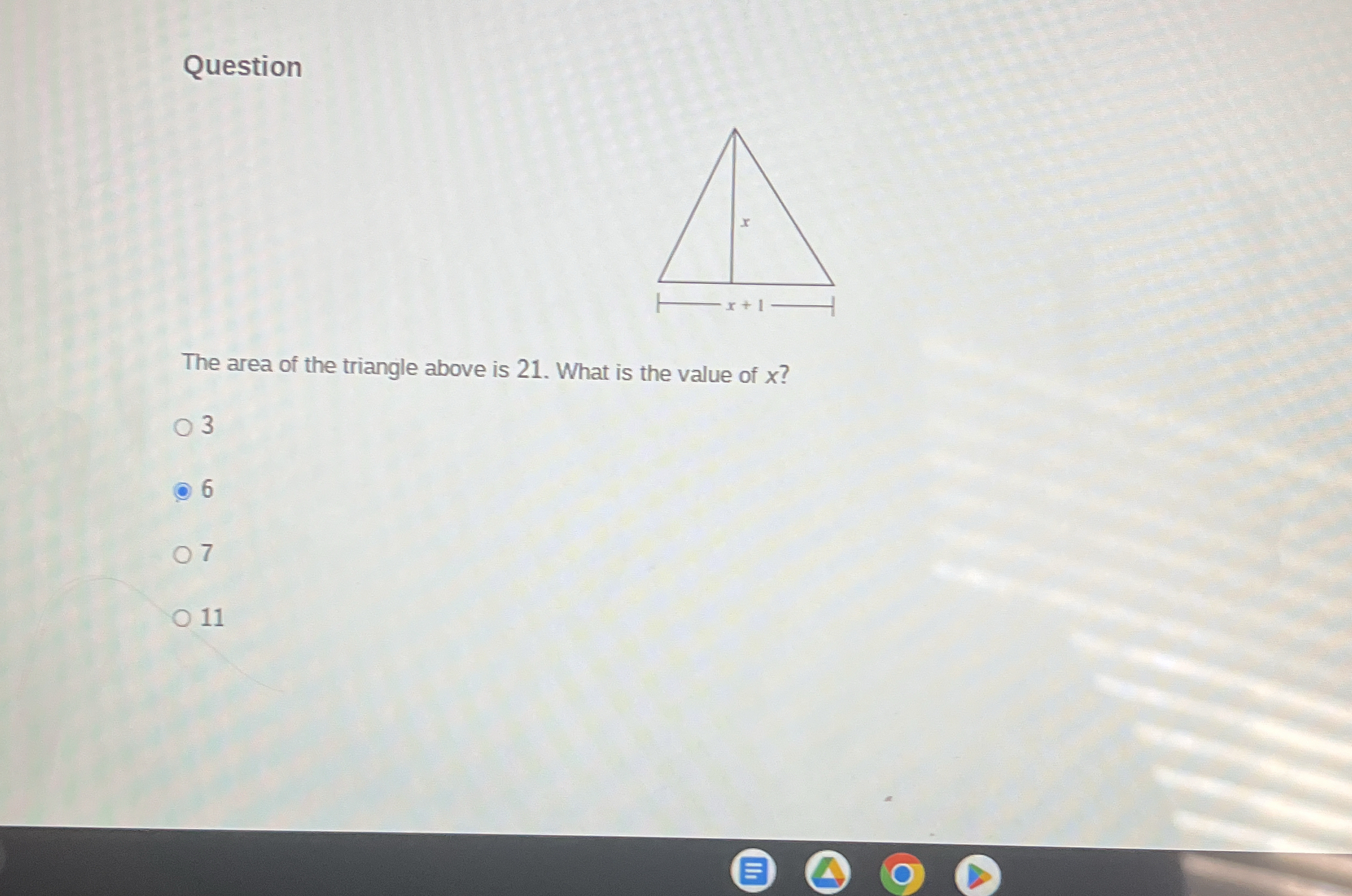
The area of the triangle above is 21. What is the value of x?
Understand the Problem
The question is asking for the value of x in a triangle whose area is given as 21. The base of the triangle is defined as (x + 1) and the height as x. To find x, we will use the formula for the area of a triangle, which is (1/2) * base * height = area.
Answer
The value of $x$ is $6$.
Answer for screen readers
The value of $x$ is $6$.
Steps to Solve
-
Write the area formula The formula for the area of a triangle is given by: $$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $$
-
Substitute known values In this problem, the area is 21, the base is $(x + 1)$, and the height is $x$. Therefore, we can write: $$ 21 = \frac{1}{2} \times (x + 1) \times x $$
-
Multiply through by 2 to eliminate the fraction To simplify, we multiply both sides of the equation by 2: $$ 42 = (x + 1) \times x $$
-
Expand the equation Now, expand the right side: $$ 42 = x^2 + x $$
-
Rearrange the equation Rearrange to set the equation to zero: $$ x^2 + x - 42 = 0 $$
-
Factor the quadratic equation We can factor the quadratic equation. We need two numbers that multiply to -42 and add to 1. Those numbers are 7 and -6: $$ (x + 7)(x - 6) = 0 $$
-
Solve for x Now, we set each factor to zero: $$ x + 7 = 0 \quad \text{or} \quad x - 6 = 0 $$
From this, we find:
- $x = -7$ (not applicable since heights can't be negative)
- $x = 6$ (valid solution)
The value of $x$ is $6$.
More Information
The area of the triangle being 21 means that the product of the base and height, when plugged into the area formula, can lead to a valid quadratic equation. By factoring, we can find the possible values for $x$.
Tips
- Forgetting to multiply by 2: Students may forget to eliminate the fraction, making the calculation more complex.
- Not checking for negative values: Occasionally, students may forget to disregard negative solutions that don’t apply in this context.
AI-generated content may contain errors. Please verify critical information