θ = 30°, θ = 45°: Find sin(θ), cos(θ), tan(θ), sin(-θ), cos(-θ), tan(-θ).
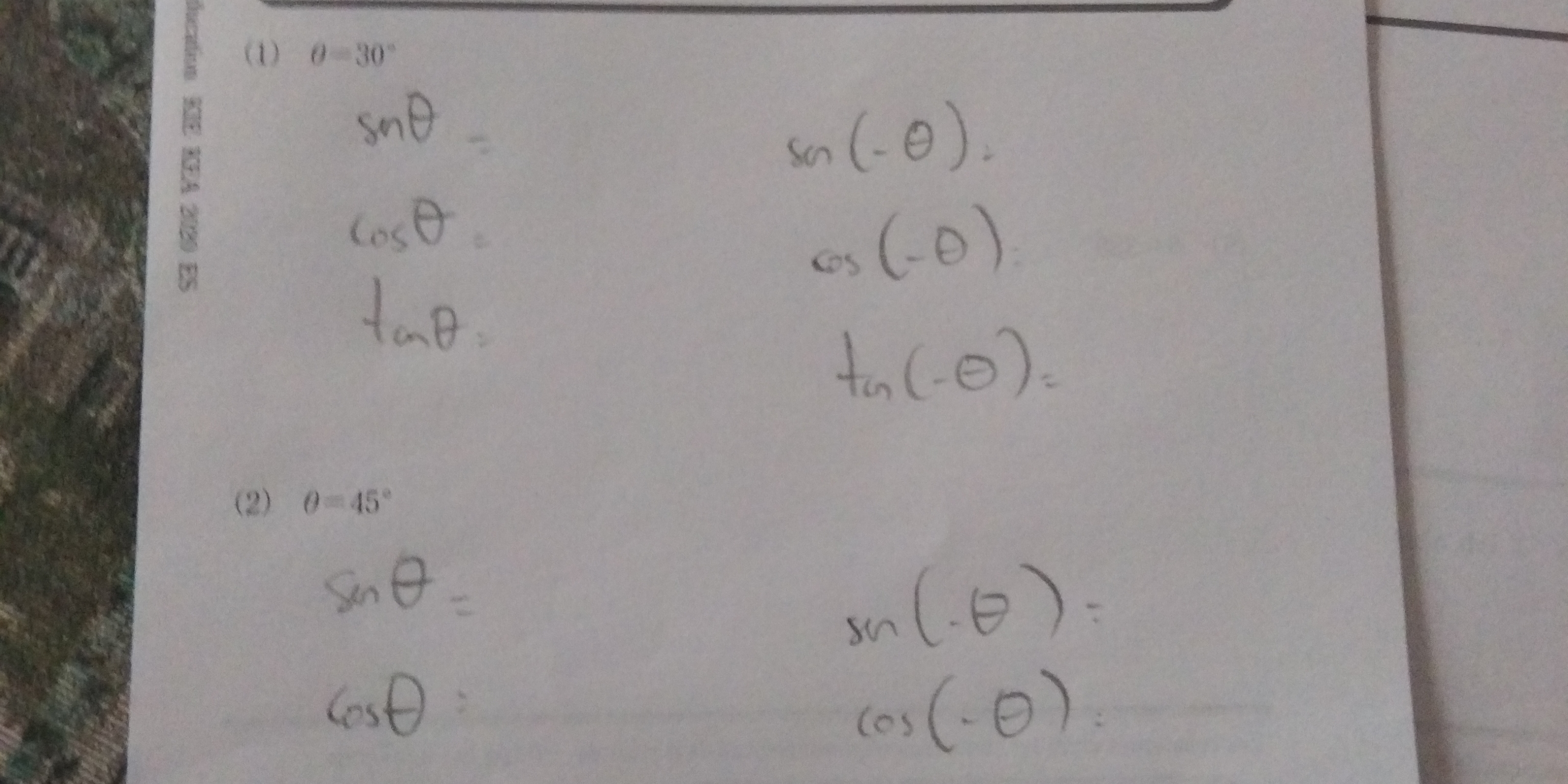
Understand the Problem
The question involves finding the values of the sine, cosine, and tangent functions for given angles of θ=30° and θ=45°, along with their values when the angle is negative. This relates to the properties of trigonometric functions and their behavior with respect to negative angles.
Answer
For \( \theta = 30° \): \( \sin(30°) = \frac{1}{2}, \cos(30°) = \frac{\sqrt{3}}{2}, \tan(30°) = \frac{1}{\sqrt{3}} \) For \( \theta = -30° \): \( \sin(-30°) = -\frac{1}{2}, \cos(-30°) = \frac{\sqrt{3}}{2}, \tan(-30°) = -\frac{1}{\sqrt{3}} \) For \( \theta = 45° \): \( \sin(45°) = \frac{\sqrt{2}}{2}, \cos(45°) = \frac{\sqrt{2}}{2}, \tan(45°) = 1 \) For \( \theta = -45° \): \( \sin(-45°) = -\frac{\sqrt{2}}{2}, \cos(-45°) = \frac{\sqrt{2}}{2}, \tan(-45°) = -1 \)
Answer for screen readers
For ( \theta = 30° ):
- ( \sin(30°) = \frac{1}{2} )
- ( \cos(30°) = \frac{\sqrt{3}}{2} )
- ( \tan(30°) = \frac{1}{\sqrt{3}} )
For ( \theta = -30° ):
- ( \sin(-30°) = -\frac{1}{2} )
- ( \cos(-30°) = \frac{\sqrt{3}}{2} )
- ( \tan(-30°) = -\frac{1}{\sqrt{3}} )
For ( \theta = 45° ):
- ( \sin(45°) = \frac{\sqrt{2}}{2} )
- ( \cos(45°) = \frac{\sqrt{2}}{2} )
- ( \tan(45°) = 1 )
For ( \theta = -45° ):
- ( \sin(-45°) = -\frac{\sqrt{2}}{2} )
- ( \cos(-45°) = \frac{\sqrt{2}}{2} )
- ( \tan(-45°) = -1 )
Steps to Solve
- Finding values for θ = 30°
We use known values of trigonometric functions:
-
The sine of 30 degrees is given by: $$ \sin(30°) = \frac{1}{2} $$
-
The cosine of 30 degrees is: $$ \cos(30°) = \frac{\sqrt{3}}{2} $$
-
The tangent of 30 degrees is: $$ \tan(30°) = \frac{\sin(30°)}{\cos(30°)} = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}} $$
- Finding values for negative angles (θ = -30°)
Using the properties of trigonometric functions for negative angles:
-
The sine function is odd: $$ \sin(-θ) = -\sin(θ) \Rightarrow \sin(-30°) = -\frac{1}{2} $$
-
The cosine function is even: $$ \cos(-θ) = \cos(θ) \Rightarrow \cos(-30°) = \frac{\sqrt{3}}{2} $$
-
The tangent function is odd: $$ \tan(-θ) = -\tan(θ) \Rightarrow \tan(-30°) = -\frac{1}{\sqrt{3}} $$
- Finding values for θ = 45°
The known values for an angle of 45 degrees are:
-
The sine of 45 degrees: $$ \sin(45°) = \frac{\sqrt{2}}{2} $$
-
The cosine of 45 degrees: $$ \cos(45°) = \frac{\sqrt{2}}{2} $$
-
The tangent of 45 degrees: $$ \tan(45°) = \frac{\sin(45°)}{\cos(45°)} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 $$
- Finding values for negative angles (θ = -45°)
Using similar properties for negative angles:
-
For sine: $$ \sin(-45°) = -\sin(45°) = -\frac{\sqrt{2}}{2} $$
-
For cosine: $$ \cos(-45°) = \cos(45°) = \frac{\sqrt{2}}{2} $$
-
For tangent: $$ \tan(-45°) = -\tan(45°) = -1 $$
For ( \theta = 30° ):
- ( \sin(30°) = \frac{1}{2} )
- ( \cos(30°) = \frac{\sqrt{3}}{2} )
- ( \tan(30°) = \frac{1}{\sqrt{3}} )
For ( \theta = -30° ):
- ( \sin(-30°) = -\frac{1}{2} )
- ( \cos(-30°) = \frac{\sqrt{3}}{2} )
- ( \tan(-30°) = -\frac{1}{\sqrt{3}} )
For ( \theta = 45° ):
- ( \sin(45°) = \frac{\sqrt{2}}{2} )
- ( \cos(45°) = \frac{\sqrt{2}}{2} )
- ( \tan(45°) = 1 )
For ( \theta = -45° ):
- ( \sin(-45°) = -\frac{\sqrt{2}}{2} )
- ( \cos(-45°) = \frac{\sqrt{2}}{2} )
- ( \tan(-45°) = -1 )
More Information
These trigonometric values are fundamental for understanding angles in the unit circle and they help in various applications, including physics, engineering, and computer graphics.
Tips
- Confusing the sine and cosine functions for negative angles; remember that sine is odd and cosine is even.
- Forgetting the values of special angles like 30° and 45°, which are frequently used.
AI-generated content may contain errors. Please verify critical information