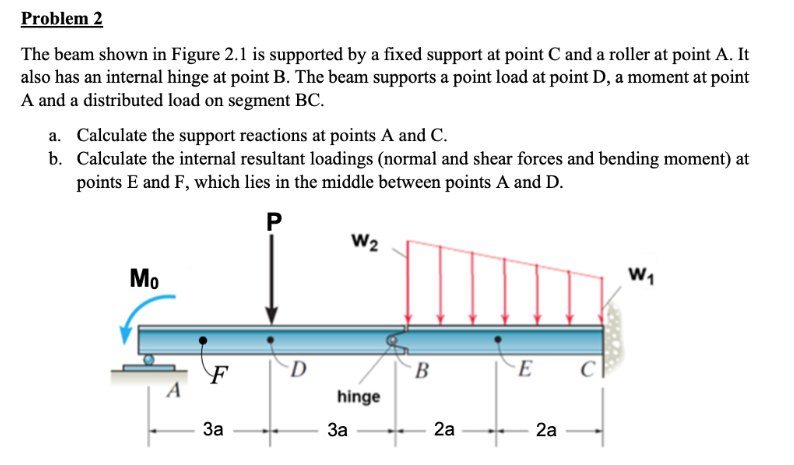
Take P = 4 kip, M0 = 5 kip-ft, w1 = 3 kip/ft, and w2 = 4 kip/ft. Take a = 3 ft. Calculate the support reactions at points A and C. Calculate the internal resultant loadings (normal... Take P = 4 kip, M0 = 5 kip-ft, w1 = 3 kip/ft, and w2 = 4 kip/ft. Take a = 3 ft. Calculate the support reactions at points A and C. Calculate the internal resultant loadings (normal and shear forces and bending moment) at points E and F. Read more

Steps to Solve

1. Identify the forces and moments acting on the beam

The beam is subjected to a point load $P$ at point $D$, a moment $M_0$ at point $A$, and distributed loads $w_1$ and $w_2$ on segments $AB$ and $BC$. The locations of the loads are specified as being at distances of $3a$, $3a$, and $2a$ from points $A$, $B$, and $C$ respectively.

2. Calculate the reactions at supports A and C

Using the equations of static equilibrium, we can sum forces in the vertical direction ($\Sigma F_y = 0$) and the moment about point A ($\Sigma M_A = 0$).

The support reactions can be denoted as:

• $R_A$: reaction at the fixed support A (vertical component)
• $R_C$: reaction at the roller support C (vertical component)

The equation becomes: $$ R_A + R_C - P - w_1 \cdot L_{w1} - w_2 \cdot L_{w2} = 0 $$

The moment equation about point A: $$ M_0 - R_C \cdot L_{C} + P \cdot d_{P} + (w_1 \cdot L_{w1}) \cdot d_{w1} + (w_2 \cdot L_{w2}) \cdot d_{w2} = 0 $$

3. Determine the specific lengths for w1 and w2

Assume:

• $L_{w1} = 3a$ (length segment from A to B)
• $L_{w2} = 2a$ (length segment from B to C)

Now we can substitute in to find $R_A$ and $R_C$.

4. Conduct shear and moment analysis at points E and F

To find shear force $V_E$ and $V_F$ and bending moment $M_E$ and $M_F$ at points E and F, use the same equilibrium equations for sections of the beam.

For point E, take a cut just to the left of E:

• Shear equation: $V_E = R_A - (W_{1 \text{ up to E}} + W_{2 \text{ up to E}})$.
• Moment equation: $M_E = M_0 + R_A \cdot d_A - w_1 \cdot L_{1} \cdot d_{w_1}$, considering distances.

For point F, the analysis follows similarly, accounting for the loads acting to the left of F.

5. Evaluate distributed loads

Compute values for the distributed loads:

• $W_{1 \text{ up to E}} = w_1 \cdot (3a) / 2$,
• $W_{2 \text{ up to E}} = w_2 \cdot (1a)$.

Use these to find reactions and resultant forces.