Solve the system of equations 2x + 5y = -9 and 3x + 4y = 4 by combining the equations.

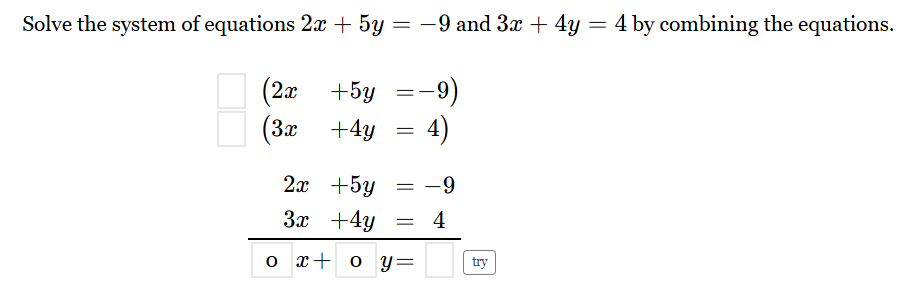
Understand the Problem

The question asks to solve a system of equations by combining them. Specifically, we need to find the values of x and y that satisfy both equations: 2x + 5y = -9 and 3x + 4y = 4.

Answer

The solution is $ x = 8, y = -5 $.

Steps to Solve

Multiply to align coefficients

To eliminate one variable, we need the coefficients of either $x$ or $y$ in both equations to match. Here, we will eliminate $y$.

Multiply the first equation, $2x + 5y = -9$, by $4$ and the second equation, $3x + 4y = 4$, by $5$:

[ 4(2x + 5y) = 4(-9) \quad \longrightarrow \quad 8x + 20y = -36 ]

[ 5(3x + 4y) = 5(4) \quad \longrightarrow \quad 15x + 20y = 20 ]

Subtract the equations

Now, we subtract the modified first equation from the modified second equation to eliminate $y$:

[ (15x + 20y) - (8x + 20y) = 20 - (-36) ]

This simplifies to:

[ 7x = 56 ]

Solve for (x)

Divide both sides by $7$:

[ x = \frac{56}{7} = 8 ]

Substitute (x) back into one of the original equations

Now, we substitute $x = 8$ back into the first original equation, $2x + 5y = -9$:

[ 2(8) + 5y = -9 ]

Solve for (y)

This simplifies to:

[ 16 + 5y = -9 ]

Now, isolate $y$:

[ 5y = -9 - 16 ] [ 5y = -25 ] [ y = \frac{-25}{5} = -5 ]

The solution to the system of equations is $x = 8$ and $y = -5$.

More Information

The values of $x$ and $y$ indicate the point at which the two lines given by the equations intersect on a Cartesian plane. The process used here is called elimination, which is one of the methods to solve systems of linear equations.

Tips

Misalignment of coefficients when multiplying equations can lead to incorrect results; ensure you multiply correctly.
Forgetting to simplify the equations before solving can make the final answer look complicated.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!