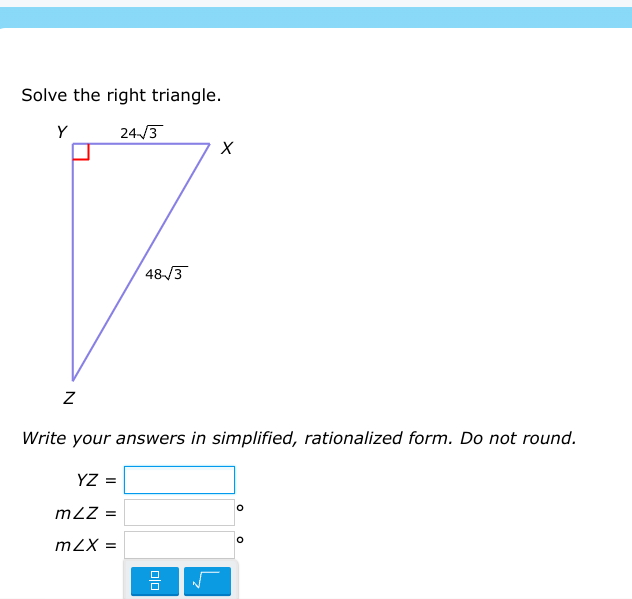
Solve the right triangle YXZ, where angle Y is the right angle, XY = 24√3, and XZ = 48√3. Find the length of YZ, the measure of angle Z, and the measure of angle X. Write your answ... Solve the right triangle YXZ, where angle Y is the right angle, XY = 24√3, and XZ = 48√3. Find the length of YZ, the measure of angle Z, and the measure of angle X. Write your answers in simplified, rationalized form. Do not round.
Understand the Problem
The question asks to solve the right triangle, given the length of one side adjacent to the right angle and the hypotenuse. Specifically, we need to find the length of the other side (YZ) and angles m∠Z and m∠X. We'll use trigonometric relationships (sine, cosine, tangent) and the Pythagorean theorem to do this.
Answer
$YZ = 72$ $m\angle Z = 30^\circ$ $m\angle X = 60^\circ$
Answer for screen readers
$YZ = 72$ $m\angle Z = 30^\circ$ $m\angle X = 60^\circ$
Steps to Solve
- Find the length of side YZ
Use the Pythagorean theorem $a^2 + b^2 = c^2$, where $c$ is the hypotenuse.
Let $XY = 24\sqrt{3}$, $XZ = 48\sqrt{3}$, and $YZ = a$. Then
$a^2 + (24\sqrt{3})^2 = (48\sqrt{3})^2$ $a^2 + 24^2 \cdot 3 = 48^2 \cdot 3$ $a^2 + 576 \cdot 3 = 2304 \cdot 3$ $a^2 + 1728 = 6912$ $a^2 = 6912 - 1728$ $a^2 = 5184$ $a = \sqrt{5184}$ $a = 72$
Therefore, $YZ = 72$.
- Find the measure of angle Z
Use the sine function: $\sin(Z) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{XY}{XZ} = \frac{24\sqrt{3}}{48\sqrt{3}} = \frac{1}{2}$
$Z = \arcsin(\frac{1}{2})$ $m\angle Z = 30^\circ$
- Find the measure of angle X
Since the sum of angles in any triangle is $180^\circ$ and $\angle Y = 90^\circ$, then $m\angle X + m\angle Z = 90^\circ$
$m\angle X = 90^\circ - m\angle Z$ $m\angle X = 90^\circ - 30^\circ$ $m\angle X = 60^\circ$
$YZ = 72$ $m\angle Z = 30^\circ$ $m\angle X = 60^\circ$
More Information
This is a special 30-60-90 triangle where sides are in the proportion $1:\sqrt{3}:2$ respectively.
Tips
A common mistake could be incorrectly identifying which side is opposite to the angle being calculated. Another mistake could be making errors in simplifying square roots. Finally, one could forget that the angles in a triangle sum up to 180 degrees exactly.
AI-generated content may contain errors. Please verify critical information