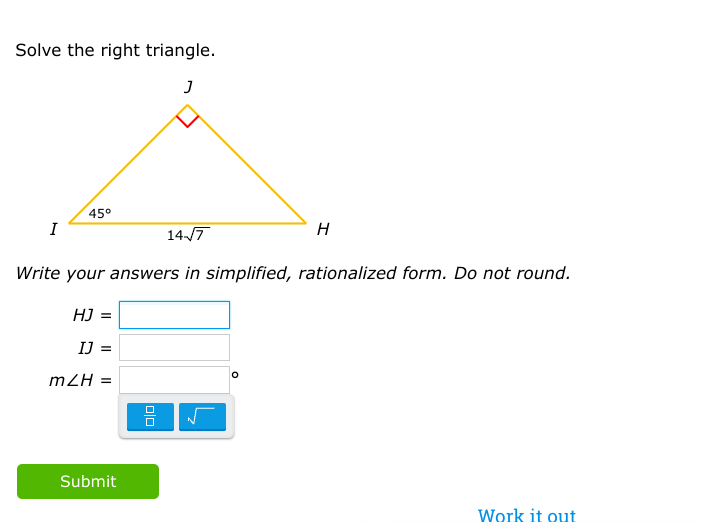
Solve the right triangle. Write your answers in simplified, rationalized form. HJ =, IJ =, m∠H = °

Steps to Solve

1. Identify Angles in the Triangle
   In a right triangle, the sum of all angles equals 180 degrees. We have one angle of 45 degrees and one right angle (90 degrees). Therefore, the remaining angle ( m\angle H ) can be calculated as:
   $$ m\angle H = 180° - 90° - 45° = 45° $$

2. Determine the Lengths of the Sides
   Since ( HJ ) is opposite ( \angle I ) (which is 45 degrees) and ( IJ ) is adjacent to it, we can use the sine function to find ( HJ ):
   $$ HJ = IH \cdot \sin(45°) $$
   Substituting ( IH = \frac{14}{\sqrt{7}} ):
   $$ HJ = \frac{14}{\sqrt{7}} \cdot \sin(45°) $$
   Since ( \sin(45°) = \frac{\sqrt{2}}{2} ), we have:
   $$ HJ = \frac{14}{\sqrt{7}} \cdot \frac{\sqrt{2}}{2} = \frac{14\sqrt{2}}{2\sqrt{7}} = \frac{7\sqrt{2}}{\sqrt{7}} = 7\sqrt{\frac{2}{7}} = \frac{7\sqrt{14}}{14} = \frac{\sqrt{14}}{2} $$

3. Calculate the Other Side Length (IJ)
   Using the cosine function, we can determine side ( IJ ):
   $$ IJ = IH \cdot \cos(45°) $$
   Substituting ( IH = \frac{14}{\sqrt{7}} ):
   $$ IJ = \frac{14}{\sqrt{7}} \cdot \cos(45°) $$
   And since ( \cos(45°) = \frac{\sqrt{2}}{2} ):
   $$ IJ = \frac{14}{\sqrt{7}} \cdot \frac{\sqrt{2}}{2} = \frac{7\sqrt{2}}{\sqrt{7}} = 7\sqrt{\frac{2}{7}} = \frac{7\sqrt{14}}{14} = \frac{7\sqrt{14}}{14} $$