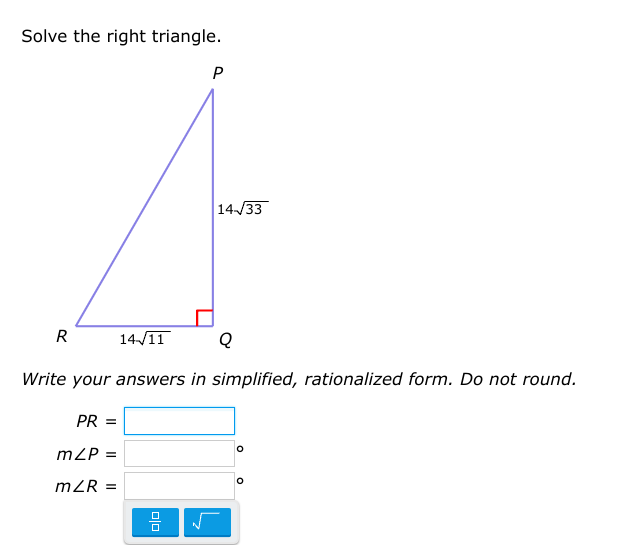
Solve the right triangle given sides $14\sqrt{11}$ and $14\sqrt{33}$. Find the length of side PR and the measures of angles P and R. Write your answers in simplified, rationalized... Solve the right triangle given sides $14\sqrt{11}$ and $14\sqrt{33}$. Find the length of side PR and the measures of angles P and R. Write your answers in simplified, rationalized form. Do not round. Read more

Steps to Solve

1. Find the length of PR using the Pythagorean Theorem

In a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as $a^2 + b^2 = c^2$. In this case, $PQ = 14\sqrt{33}$ and $RQ = 14\sqrt{11}$, and we want to find $PR$. So, $PR^2 = PQ^2 + RQ^2$

2. Calculate $PR^2$

Substitute the given values: $PR^2 = (14\sqrt{33})^2 + (14\sqrt{11})^2$ $PR^2 = 14^2 \cdot 33 + 14^2 \cdot 11 $ $PR^2 = 196 \cdot 33 + 196 \cdot 11$ $PR^2 = 6468 + 2156$ $PR^2 = 8624$

3. Find $PR$

Take the square root of both sides: $PR = \sqrt{8624}$ Simplify the square root: $PR = \sqrt{196 \cdot 44} = \sqrt{196 \cdot 4 \cdot 11} = 14 \cdot 2 \cdot \sqrt{11} = 28\sqrt{11}$

4. Find the measure of angle P

We can use the tangent function: $\tan(P) = \frac{RQ}{PQ} = \frac{14\sqrt{11}}{14\sqrt{33}}$ Simplify: $\tan(P) = \frac{\sqrt{11}}{\sqrt{33}} = \frac{\sqrt{11}}{\sqrt{11} \cdot \sqrt{3}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$ $P = \arctan(\frac{\sqrt{3}}{3}) = 30^\circ$

5. Find the measure of angle R

Since the sum of angles in a triangle is $180^\circ$ and angle Q is $90^\circ$, $P + R = 90^\circ$. Thus, $R = 90^\circ - P = 90^\circ - 30^\circ = 60^\circ$.