Solve the following system of inequalities graphically on the set of axes below. State the coordinates of a point in the solution set.
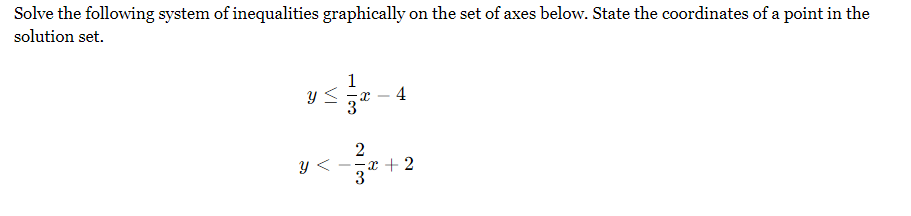
Understand the Problem
The question is asking to solve a system of inequalities graphically and to identify a point within the solution set. This involves plotting the inequalities on a graph and finding the region that satisfies both inequalities.
Answer
The coordinates of a point in the solution set are (0, -5).
Answer for screen readers
A point in the solution set is (0, -5).
Steps to Solve
- Rewrite the inequalities We have two inequalities to rewrite for easier graphing:
- The first inequality is $y \leq \frac{1}{3}x - 4$.
- The second inequality is $y < -\frac{2}{3}x + 2$.
- Graph the first inequality To graph $y = \frac{1}{3}x - 4$, plot the line by finding the y-intercept and slope:
- The y-intercept is at (0, -4).
- The slope is $\frac{1}{3}$, meaning from the y-intercept you move up 1 unit and right 3 units to find another point (3, -3).
Since the inequality is $\leq$, shade below the line.
- Graph the second inequality To graph $y = -\frac{2}{3}x + 2$, again start with finding points:
- The y-intercept is at (0, 2).
- The slope is $-\frac{2}{3}$, moving down 2 units and right 3 units leads to another point (3, 0).
Since the inequality is $<$, shade below the line, and the line itself will be dashed (not included).
-
Identify the solution region The solution region is where the shaded areas of both inequalities overlap. This will be below both lines.
-
Find a point in the solution set Choose a point that lies within the overlapping shaded region. For example, the point (0, -5) is a suitable point since it is located below both lines.
A point in the solution set is (0, -5).
More Information
Graphical methods are often used to solve systems of inequalities to visually identify the solution set. The overlapping shaded area represents all the points that satisfy both inequalities.
Tips
- Failing to distinguish between solid and dashed lines based on the type of inequality (solid for $\leq$, dashed for $<$).
- Not correctly shading the region below the lines can lead to an incorrect representation of the solution set.
AI-generated content may contain errors. Please verify critical information