Solve the following system of equations: x - y = 10 and x = 2y + 1.
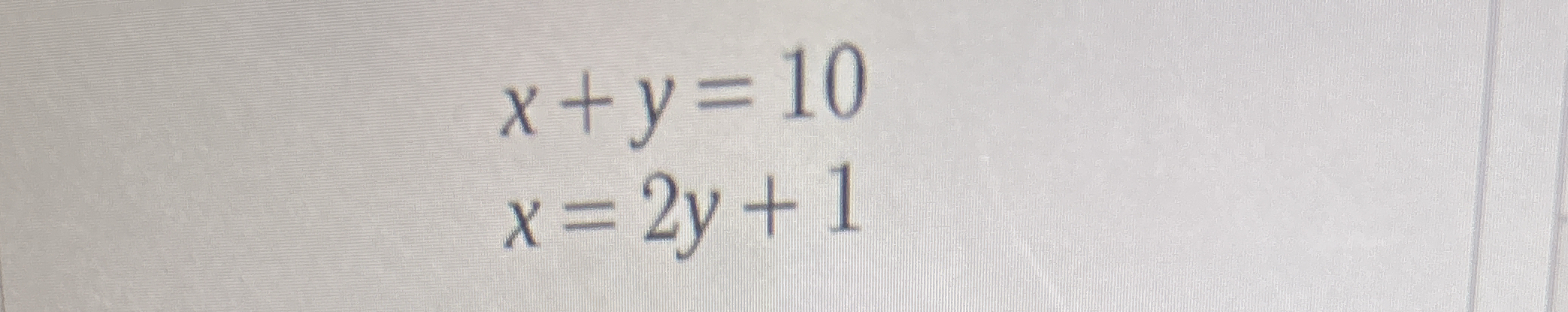
Understand the Problem
The question is asking to solve a system of linear equations represented as two equations: x - y = 10 and x = 2y + 1. We aim to find the values of x and y that satisfy both equations simultaneously.
Answer
The solution is $x = 19$ and $y = 9$.
Answer for screen readers
The solution to the system of equations is $x = 19$ and $y = 9$.
Steps to Solve
-
Rearrange the first equation We can express $x$ in terms of $y$ from the first equation: $$ x = y + 10 $$
-
Substitute into the second equation Next, substitute the expression for $x$ into the second equation: $$ y + 10 = 2y + 1 $$
-
Solve for y Now, we will isolate $y$: $$ 10 - 1 = 2y - y $$ This simplifies to: $$ 9 = y $$
-
Substitute to find x Now, substitute $y$ back into the expression for $x$: $$ x = 9 + 10 $$ So: $$ x = 19 $$
The solution to the system of equations is $x = 19$ and $y = 9$.
More Information
This system of linear equations represents two lines in a Cartesian plane that intersect at the point $(19, 9)$. This point is the unique solution to the system, meaning it satisfies both equations simultaneously.
Tips
- Misunderstanding substitution: Ensure to substitute the correct expression for $x$ into the second equation.
- Arithmetic errors: Double-check calculations when isolating variables, especially while performing addition or subtraction.
AI-generated content may contain errors. Please verify critical information