Solve the following quadratic equation for all values of x in simplest form: 7 - x² = 6.
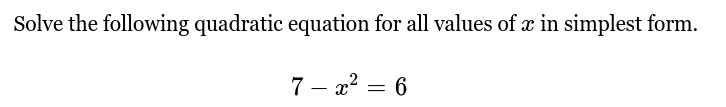
Understand the Problem
The question is asking to solve a quadratic equation, specifically 7 - x² = 6, for all possible values of x. The solution needs to be presented in its simplest form.
Answer
The solutions are $x = 1$ and $x = -1$.
Answer for screen readers
The solutions to the equation $7 - x^2 = 6$ are $x = 1$ and $x = -1$.
Steps to Solve
- Rearrange the equation
First, we want to isolate the term with $x$. Start by moving 6 to the left side:
$$ 7 - 6 = x^2 $$
This simplifies to:
$$ 1 = x^2 $$
- Take the square root of both sides
To solve for $x$, take the square root of both sides. Remember that taking the square root produces both positive and negative solutions:
$$ x = \pm \sqrt{1} $$
Thus,
$$ x = 1 \quad \text{or} \quad x = -1 $$
- Present the solution
We now have the solutions for $x$. They are:
$$ x = 1 \quad \text{and} \quad x = -1 $$
The solutions to the equation $7 - x^2 = 6$ are $x = 1$ and $x = -1$.
More Information
Quadratic equations can often have two solutions because of the nature of square roots. In this case, both $1$ and $-1$ are valid because they satisfy the original equation.
Tips
- Forgetting to include both the positive and negative roots when taking the square root.
- Mistaking the operation when rearranging the equation (e.g., failing to correctly move terms).
AI-generated content may contain errors. Please verify critical information