Solve the following quadratic equation for all values of x in simplest form: 2(x + 4)² + 15 = 17.
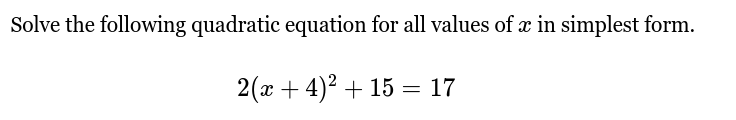
Understand the Problem
The question is asking to solve the quadratic equation given in the image for all values of x and to express the solutions in their simplest form.
Answer
$x = -3 \quad \text{and} \quad x = -5$
Answer for screen readers
The solutions to the equation $2(x + 4)^2 + 15 = 17$ are $x = -3$ and $x = -5$.
Steps to Solve
- Isolate the quadratic term
Start by subtracting 15 from both sides of the equation to isolate the quadratic term: $$ 2(x + 4)^2 + 15 - 15 = 17 - 15 $$
This simplifies to: $$ 2(x + 4)^2 = 2 $$
- Divide by the coefficient of the square
Next, divide both sides by 2: $$ \frac{2(x + 4)^2}{2} = \frac{2}{2} $$
This simplifies to: $$ (x + 4)^2 = 1 $$
- Take the square root of both sides
Next, take the square root of both sides. Remember to consider both the positive and negative roots: $$ x + 4 = \pm 1 $$
- Solve for x
Now, solve each equation separately.
For the positive root: $$ x + 4 = 1 \ x = 1 - 4 \ x = -3 $$
For the negative root: $$ x + 4 = -1 \ x = -1 - 4 \ x = -5 $$
- List the solutions
The solutions to the quadratic equation are: $$ x = -3 \quad \text{and} \quad x = -5 $$
The solutions to the equation $2(x + 4)^2 + 15 = 17$ are $x = -3$ and $x = -5$.
More Information
Quadratic equations often have two solutions, and taking the square root introduces both positive and negative possibilities. Here, we confirmed that both roots are valid solutions.
Tips
- Forgetting to consider both the positive and negative square roots when taking the square root of both sides.
- Misapplying the distributive property or simplifying incorrectly when manipulating the equation.
AI-generated content may contain errors. Please verify critical information