Solve the equation x² - 3x + 8 = 0.
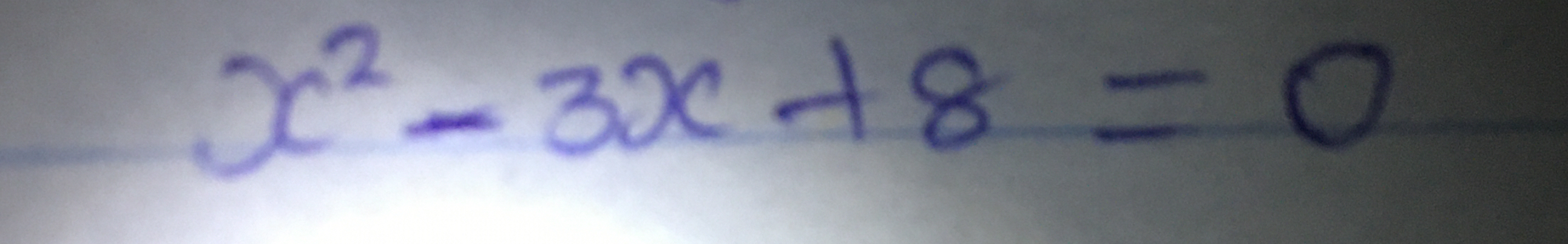
Understand the Problem
The question is asking for a solution to the quadratic equation provided, which is in the form of x² - 3x + 8 = 0. We will find the values of x that satisfy this equation.
Answer
The solutions are $x_1 = \frac{3 + i\sqrt{23}}{2}$ and $x_2 = \frac{3 - i\sqrt{23}}{2}$.
Answer for screen readers
The roots of the equation are: $$ x_1 = \frac{3 + i\sqrt{23}}{2}, \quad x_2 = \frac{3 - i\sqrt{23}}{2} $$
Steps to Solve
-
Identify the coefficients In the equation $x^2 - 3x + 8 = 0$, identify the coefficients ( a = 1 ), ( b = -3 ), and ( c = 8 ).
-
Calculate the discriminant The discriminant ( D ) is calculated using the formula: $$ D = b^2 - 4ac $$ Substituting the values: $$ D = (-3)^2 - 4 \cdot 1 \cdot 8 $$ $$ D = 9 - 32 $$ $$ D = -23 $$
-
Determine the nature of the roots Since the discriminant ( D ) is negative, this means the quadratic equation has no real roots. Instead, it has two complex roots.
-
Use the quadratic formula The quadratic formula is given by: $$ x = \frac{-b \pm \sqrt{D}}{2a} $$ Substituting the values: $$ x = \frac{-(-3) \pm \sqrt{-23}}{2 \cdot 1} $$ $$ x = \frac{3 \pm i\sqrt{23}}{2} $$
-
Express the final roots The two complex roots can be expressed as: $$ x_1 = \frac{3 + i\sqrt{23}}{2} $$ $$ x_2 = \frac{3 - i\sqrt{23}}{2} $$
The roots of the equation are: $$ x_1 = \frac{3 + i\sqrt{23}}{2}, \quad x_2 = \frac{3 - i\sqrt{23}}{2} $$
More Information
The roots are complex because the discriminant is negative. In contexts like physics or engineering, complex roots can indicate oscillations or cyclic behavior where real solutions aren’t applicable.
Tips
- Miscalculating the discriminant can lead to incorrect conclusions about the nature of the roots.
- Forgetting to include the imaginary unit ( i ) when dealing with negative discriminants can cause confusion.
AI-generated content may contain errors. Please verify critical information