Solve the differential equation (e^y - 1)y' = 2 + cos x.
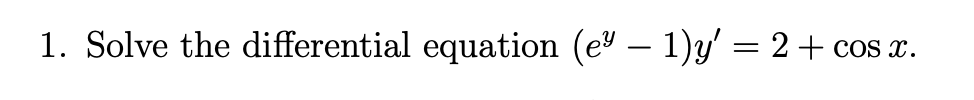
Understand the Problem
The question is asking to solve a given differential equation involving the variable y and its derivative y'. The goal is to find the function y in terms of x.
Answer
The implicit solution is given by: $$ e^y - y - 2x - \sin x - C = 0 $$
Answer for screen readers
The solution to the differential equation is given by the implicit relation: $$ e^y - y - 2x - \sin x - C = 0 $$
Steps to Solve
-
Rewrite the differential equation To isolate $y'$ (the derivative of $y$), rewrite the equation as: $$ y' = \frac{2 + \cos x}{e^y - 1} $$
-
Separate variables Separate the variables so that all terms involving $y$ are on one side and those involving $x$ are on the other: $$ (e^y - 1) dy = (2 + \cos x) dx $$
-
Integrate both sides Integrate both sides to find the relationship between $y$ and $x$: $$ \int (e^y - 1) dy = \int (2 + \cos x) dx $$
-
Calculate the integrals The integral on the left is: $$ \int (e^y - 1) dy = e^y - y $$ The integral on the right is: $$ \int (2 + \cos x) dx = 2x + \sin x + C $$
-
Combine the results Set the results from both integrals equal to each other: $$ e^y - y = 2x + \sin x + C $$
-
Solve for y While it may not be possible to explicitly solve for $y$ in terms of elementary functions, the relationship can be expressed as: $$ e^y - y - 2x - \sin x - C = 0 $$
The solution to the differential equation is given by the implicit relation: $$ e^y - y - 2x - \sin x - C = 0 $$
More Information
This solution expresses the relationship between $y$ and $x$ implicitly, according to the original differential equation. The constant ( C ) can be determined if an initial condition is provided.
Tips
- Forgetting to properly separate the variables.
- Not integrating both sides correctly or missing the integration constant ( C ).
- Confusing the terms while integrating, particularly the $e^y$ term.
AI-generated content may contain errors. Please verify critical information