Solve the differential equation 4x^3y + x^4y' = sin^3 x.
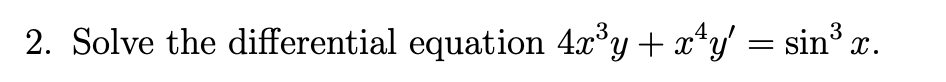
Understand the Problem
The question is asking to solve a specific differential equation involving the variables x and y, which is expressed in the form 4x³y + x⁴y' = sin³x.
Answer
$$ y = \frac{-\frac{1}{3} \cos(3x) + C}{x^4} $$
Answer for screen readers
The solution to the differential equation is given by: $$ y = \frac{-\frac{1}{3} \cos(3x) + C}{x^4} $$
Steps to Solve
-
Rearranging the differential equation We start with the equation: $$ 4x^3y + x^4y' = \sin^3 x $$ Rearranging it gives: $$ x^4y' = \sin^3 x - 4x^3y $$
-
Separating variables Next, we will express the equation in a form suitable for separating variables: $$ y' = \frac{\sin^3 x - 4x^3y}{x^4} $$ This implies: $$ \frac{dy}{dx} = \frac{\sin^3 x}{x^4} - \frac{4y}{x} $$
-
Finding an integrating factor To solve this linear first-order differential equation, we can find the integrating factor: The equation can be rewritten as: $$ y' + \frac{4}{x}y = \frac{\sin^3 x}{x^4} $$ The integrating factor $\mu(x)$ is given by: $$ \mu(x) = e^{\int \frac{4}{x} dx} = e^{4 \ln |x|} = |x|^4 $$
-
Multiplying the whole equation by the integrating factor Now, we multiply the entire equation by the integrating factor: $$ |x|^4 y' + 4|x|^3 y = |x|^4 \cdot \frac{\sin^3 x}{x^4} $$ This simplifies to: $$ |x|^4 y' + 4|x|^3 y = \sin^3 x $$
-
Expressing the left side as a derivative The left side can be expressed as the derivative of a product: $$ \frac{d}{dx}(|x|^4 y) = \sin^3 x $$
-
Integrating both sides Now we integrate both sides: $$ \int \frac{d}{dx}(|x|^4 y) , dx = \int \sin^3 x , dx $$ This gives: $$ |x|^4 y = -\frac{1}{3} \cos(3x) + C $$
-
Solving for y Finally, we isolate (y): $$ y = \frac{-\frac{1}{3} \cos(3x) + C}{|x|^4} $$
The solution to the differential equation is given by: $$ y = \frac{-\frac{1}{3} \cos(3x) + C}{x^4} $$
More Information
This is a first-order linear ordinary differential equation which was solved using the method of integrating factors. The resulting solution contains a constant of integration, ( C ), which can be determined if an initial condition is provided.
Tips
- Forgetting to apply the integrating factor correctly to both sides of the equation.
- Not simplifying before integrating; always check if there is a simpler form to work with.
- Confusing the roles of dependent and independent variables while rearranging the equation.
AI-generated content may contain errors. Please verify critical information