Solve for a.
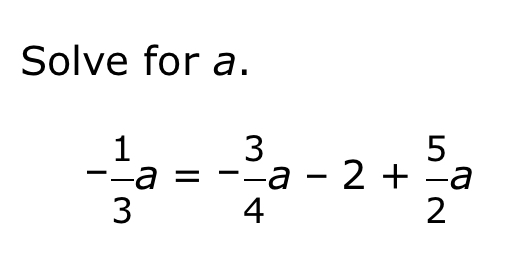
Understand the Problem
The question is asking to solve the equation for the variable 'a'. This involves algebraic manipulation to isolate 'a' on one side of the equation.
Answer
\( a = \frac{24}{25} \)
Answer for screen readers
The value of ( a ) is ( \frac{24}{25} ).
Steps to Solve
- Write the equation clearly
The equation is given by: $$ -\frac{1}{3}a = -\frac{3}{4}a - 2 + \frac{5}{2}a $$
- Combine like terms on the right side
Let's simplify the right side of the equation:
- Combine $-\frac{3}{4}a$ and $\frac{5}{2}a$.
Convert $\frac{5}{2}$ into a fraction with a common denominator of 4: $$ \frac{5}{2} = \frac{10}{4} $$
Now, we can combine: $$ -\frac{3}{4}a + \frac{10}{4}a = \frac{7}{4}a $$
So, the equation now looks like: $$ -\frac{1}{3}a = \frac{7}{4}a - 2 $$
- Move the terms involving 'a' to one side
Add $\frac{1}{3}a$ to both sides of the equation: $$ 0 = \frac{7}{4}a + \frac{1}{3}a - 2 $$
- Find a common denominator for the 'a' terms
The common denominator for 4 and 3 is 12. Convert the terms: $$ \frac{7}{4}a = \frac{21}{12}a $$ $$ \frac{1}{3}a = \frac{4}{12}a $$
Combine these: $$ 0 = \left(\frac{21}{12}a + \frac{4}{12}a\right) - 2 $$ $$ 0 = \frac{25}{12}a - 2 $$
- Isolate 'a'
Add 2 to both sides: $$ 2 = \frac{25}{12}a $$
Now, multiply both sides by the reciprocal of $\frac{25}{12}$, which is $\frac{12}{25}$: $$ a = 2 \times \frac{12}{25} $$
- Calculate the value of 'a'
Compute: $$ a = \frac{24}{25} $$
The value of ( a ) is ( \frac{24}{25} ).
More Information
This process involved combining like terms and isolating the variable using algebraic operations. The solution shows that ( a ) is a fractional value, indicating a precise relationship between the variables in the equation.
Tips
- Confusing the signs when moving terms to one side.
- Forgetting to find a common denominator when combining fractions.
AI-generated content may contain errors. Please verify critical information